题目内容
11.化简求值:①(2x+3y)2-(2x+y)•(2x-y),其中x=$\frac{1}{3}$,y=-$\frac{1}{2}$
②$\frac{{a}^{2}}{a-1}$-a-1,其中a=2.
分析 ①原式利用完全平方公式,以及平方差公式化简,去括号合并得到最简结果,把x与y的值代入计算即可求出值;
②原式通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:①(2x+3y)2-(2x+y)(2x-y)
=4x2+12xy+9y2-(4x2-y2)
=4x2+12xy+9y2-4x2+y2
=12xy+10y2,
当x=$\frac{1}{3}$,y=-$\frac{1}{2}$时,原式=-2+2.5=0.5;
②原式=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$=$\frac{1}{a-1}$,
当a=2时,原式=1.
点评 此题考查了分式的化简求值,以及整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 经过一点只能作一条直线 | B. | 射线、线段都是直线的一部分 | ||
| C. | 延长线段AB到点C使AC=BC | D. | 画直线AB=5cm |
3.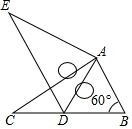 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )| A. | 0.5 | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
1.已知m、n是方程x2+3x-2=0的两个实数根,则m2+4m+n+2mn的值为( )
| A. | 1 | B. | 3 | C. | -5 | D. | -9 |
 已知:如图,∠1+∠D=90°,BE∥FC,且DF⊥BE与点G,并分别与AB、CD交于点F、D.求证:AB∥CD.(完成证明并写出推理依据)
已知:如图,∠1+∠D=90°,BE∥FC,且DF⊥BE与点G,并分别与AB、CD交于点F、D.求证:AB∥CD.(完成证明并写出推理依据)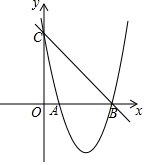 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).