题目内容
9.下列计算正确的是( )| A. | $\frac{b}{a}+\frac{d}{c}=\frac{b+d}{a+c}$ | B. | $\frac{b}{a}÷\frac{d}{c}=\frac{bd}{ac}$ | C. | $\sqrt{{a^2}+{b^2}}=a+b$ | D. | $\sqrt{{{(-\frac{1}{2})}^2}}=\frac{1}{2}$ |
分析 A、原式通分并利用同分母分式的加法法则计算得到结果,即可做出判断;
B、原式利用除法法则变形,计算得到结果,即可做出判断;
C、原式不能化简,错误;
D、原式利用二次根式的性质及绝对值的代数意义化简得到结果,即可做出判断.
解答 解:A、原式=$\frac{bc+ad}{ac}$,错误;
B、原式=$\frac{b}{a}$•$\frac{c}{d}$=$\frac{bc}{ad}$,错误;
C、原式为最简结果,错误;
D、原式=|-$\frac{1}{2}$|=$\frac{1}{2}$.
故选D.
点评 此题考查了分式的乘除法,分式的加减法,以及二次根式的性质与化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.一次函数y=ax+1与y=bx-2的图象交于x轴上一点,那么a:b等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 以上答案都不对 |
17.下列命题中,是真命题的是( )
| A. | 如果∠1+∠2=180°,那么∠1与∠2互为邻补角 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
4. 如图,平行四边形ABCD中,已知∠AOB=90°,AC=8cm,AD=5cm,则BD的长为( )
如图,平行四边形ABCD中,已知∠AOB=90°,AC=8cm,AD=5cm,则BD的长为( )
 如图,平行四边形ABCD中,已知∠AOB=90°,AC=8cm,AD=5cm,则BD的长为( )
如图,平行四边形ABCD中,已知∠AOB=90°,AC=8cm,AD=5cm,则BD的长为( )| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |
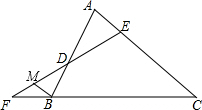 已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.