如图.平行四边形ABCD中.已知∠AOB=90°.AC=8cm.AD=5cm.则BD的长为( )A．3cmB．4cmC．6cmD．8cm 题目和参考答案——青夏教育精英家教网—

题目内容

4．

如图，平行四边形ABCD中，已知∠AOB=90°，AC=8cm，AD=5cm，则BD的长为（　　）

A．

3cm

B．

4cm

C．

6cm

D．

8cm

分析由平行四边形ABCD中，AC=8cm，根据平行四边形的对角线互相平分，即可求得OA的长，然后由勾股定理求得OB的长，继而求得答案．

解答解：∵四边形ABCD是平行四边形，
∴OA=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4（cm），
∵∠AOB=90°，
∴∠AOD=180°-∠AOB=90°，
∴OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3（cm），
∴BD=2OD=6cm．
故选C．

点评此题考查了平行四边形的性质以及勾股定理．注意平行四边形的对角线互相平分．

练习册系列答案

15．如果三角形的两边分别为4和6，那么连接该三角形三边中点所得三角形的周长可能是（　　）

12．绝对值小于6.6的所有整数的和是0．

19．

计算机中的堆栈是一些连续的存储单元，在每个堆栈中数据的存入、取出按照“先进后出”的原则，如图，堆栈（1）中的2个连续存储单元已依次存入数据b，a，取出数据的顺序是a，b；堆栈（2）的3个连续存储单元已依次存入数据e，d，c，取出数据的顺序是c，d，e，现在要从这两个堆栈中取出5个数据（每次取出1个数据），则取出的数据按abcde的顺序的概率为$\frac{1}{10}$．

9．下列计算正确的是（　　）

A．

$\frac{b}{a}+\frac{d}{c}=\frac{b+d}{a+c}$

B．

$\frac{b}{a}÷\frac{d}{c}=\frac{bd}{ac}$

C．

$\sqrt{{a^2}+{b^2}}=a+b$

D．

$\sqrt{{{（-\frac{1}{2}）}^2}}=\frac{1}{2}$

16．计算并观察下列式子，探索它们的规律，并解决问题．
$（\sqrt{3}+\sqrt{1}）（\sqrt{3}-\sqrt{1}）$=2．
$（\sqrt{5}+\sqrt{3}）（\sqrt{5}-\sqrt{3}）$=2．
$（\sqrt{7}+\sqrt{5}）（\sqrt{7}-\sqrt{5}）$=2．
…
（1）试用正整数n表示这个规律，并加以证明；
（2）求$\frac{1}{{\sqrt{3}+1}}+\frac{1}{{\sqrt{5}+\sqrt{3}}}+\frac{1}{{\sqrt{7}+\sqrt{5}}}+…+\frac{1}{{\sqrt{121}+\sqrt{119}}}$的值．

13．若关于x的方程（k+3）x²+kx-3=0是一元一次方程，则k=-3；若它是一元二次方程，则k≠-3．

14．

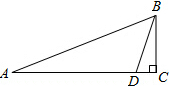一艘军舰从点A向位于正东方向的C岛航行，在点A处测得B岛在其北偏东70°方向，航行75千米到达点D处，测得B岛在其北偏东20°，继续航行5千米到达C岛，此时接到通知，要求这艘军舰在半小时内赶到正北方向的B岛执行任务，则这艘军舰的航行速度至少为多少才能按时赶到B岛？

试题分类