题目内容
14.已知反比例函数$y=\frac{k}{x}$的图象与一次函数y=x-1的图象的一个交点的横坐标是2.(1)求k的值;
(2)根据反比例函数的图象,指出当x<2时,y的取值范围.
分析 (1)把x=2代入一次函数的解析式,即可求得交点坐标,然后利用待定系数法即可求得k的值.
(2)利用反比例函数的解析式求出x=2的点,利用图图象求得答案.
解答 解:(1)在y=x-1中,令x=2,
解得y=1,
则交点坐标是:(2,1),
代入$y=\frac{k}{x}$得:k=2.
(2)∵当x=2时,y=1,
如图:
∴当x<2时,y的取值范围是y>1.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
5.下列等式从左到右的变形是因式分解的是( )
| A. | 6a3b=3a2•2ab | B. | (x+2)(x-2)=x2-4 | ||
| C. | 2x2+4x-3=2x(x+2)-3 | D. | ax-ay=a(x-y) |
2.下列运算正确的是( )
| A. | (a2)3=a6 | B. | (ab)2=ab2 | C. | a2+a2=a4 | D. | a•a2=a2 |
9.下列计算正确的是( )
| A. | $\frac{b}{a}+\frac{d}{c}=\frac{b+d}{a+c}$ | B. | $\frac{b}{a}÷\frac{d}{c}=\frac{bd}{ac}$ | C. | $\sqrt{{a^2}+{b^2}}=a+b$ | D. | $\sqrt{{{(-\frac{1}{2})}^2}}=\frac{1}{2}$ |
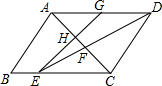 如图,已知?ABCD,DE平分∠ADC分别交BC、AC于点E、F,G是AD中点,EG交AC于点H.若AB=4,AD=6.求
如图,已知?ABCD,DE平分∠ADC分别交BC、AC于点E、F,G是AD中点,EG交AC于点H.若AB=4,AD=6.求