题目内容
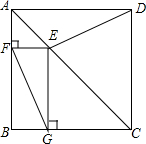 如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB.
如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB.(1)试猜测DE与FG关系如何?并说明理由
(2)如果正方形ABCD的边长为4cm,求四边形BGEF的周长.
考点:全等三角形的判定与性质,矩形的判定与性质,正方形的性质
专题:
分析:(1)如图,作辅助线;首先证明△ABE≌△ADE,得到BE=DE;证明四边形EFBG为矩形,得到FG=BE,即可解决问题.
(2)证明AF=EF,进而得到BF+EF=BF+AF=AB=4;证明四边形BGEF的周长=2(BF+EF),即可解决问题.
(2)证明AF=EF,进而得到BF+EF=BF+AF=AB=4;证明四边形BGEF的周长=2(BF+EF),即可解决问题.
解答: 解:(1)如图,连接BE;
解:(1)如图,连接BE;
∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC;
在△ABE与△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
∵EG⊥BC,EF⊥AB,∠FBG=90°,
∴四边形EFBG为矩形,
∴FG=BE,
∴DE=FG.
(2)∵∠EAF=45°,EF⊥AF,
∴∠AEF=∠EAF=45°,
∴AF=EF,BF+EF=BF+AF=AB=4,
∵四边形BGEF为矩形,
∴四边形BGEF的周长=2(BF+EF)=8(cm).
 解:(1)如图,连接BE;
解:(1)如图,连接BE;∵四边形ABCD为正方形,
∴AB=AD,∠BAC=∠DAC;
在△ABE与△ADE中,
|
∴△ABE≌△ADE(SAS),
∴BE=DE;
∵EG⊥BC,EF⊥AB,∠FBG=90°,
∴四边形EFBG为矩形,
∴FG=BE,
∴DE=FG.
(2)∵∠EAF=45°,EF⊥AF,
∴∠AEF=∠EAF=45°,
∴AF=EF,BF+EF=BF+AF=AB=4,
∵四边形BGEF为矩形,
∴四边形BGEF的周长=2(BF+EF)=8(cm).
点评:该题主要考查了正方形的性质、矩形的判定及其性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线;应牢固掌握全等三角形的判定及其性质等几何知识点.

练习册系列答案
相关题目
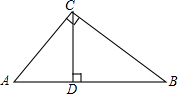 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证: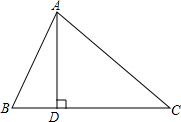 如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.
如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm. 要焊接一个如图所示的钢架,大约需要多少米的钢材(精确到0.1m)?(图中的△BCE和△ABD都是等腰直角三角形,CD=8m,BE=3m)
要焊接一个如图所示的钢架,大约需要多少米的钢材(精确到0.1m)?(图中的△BCE和△ABD都是等腰直角三角形,CD=8m,BE=3m)