题目内容
3.在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2-4ax+c(a≠0)图象的对称轴上的概率.
分析 (1)利用树状图展示所有6种等可能的情况;
(2)先利用二次函数的性质求出抛物线的对称轴方程,再在上述6种可能的结果数中找出点落在对称轴上的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有6种等可能的情况,分别为(1,2),(1,3),(2,1),(2,3),(3,1),(3,2);
(2)抛物线的对称轴为直线x=-$\frac{-4a}{2a}$=2,
共有6种等可能的情况,其中点在对称轴上的情况有2种,分别为(2,1),(2,3),
∴P(点(x,y)在对称轴上)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了二次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.把19547精确到千位的近似数是( )
| A. | 1.95×103 | B. | 1.95×104 | C. | 2.0×104 | D. | 1.9×104 |
14.若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为( )
| A. | 1:9 | B. | 1:3 | C. | 1:2 | D. | 1:$\sqrt{3}$ |
11.若$\frac{x}{y}$=$\frac{4}{5}$,则$\frac{2x-y}{x+y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
8.点P(2,-3)关于x轴对称的点是( )
| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
13.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{{a}^{2}x+{a}^{3}y}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{18}$ | D. | $\sqrt{{a}^{2}-{b}^{2}}$ |
 如图,AB为⊙O的弦,AB=8,OA=5,OP⊥AB于P,则OP=3.
如图,AB为⊙O的弦,AB=8,OA=5,OP⊥AB于P,则OP=3.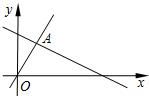 如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为x<1.
如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为x<1.