题目内容
9．
如图，滑雪场有一坡角α为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底垂直高度AB的长为（ ）| A． | 200tan20°米 | B． | $\frac{200}{sin20°}$米 | C． | 200sin20°米 | D． | 200cos20°米 |
分析 根据正弦的定义进行解答即可．
解答 解：∵sin∠C=$\frac{AB}{AC}$，
∴AB=AC•sin∠C=200sin20°，
故选：C．
点评 本题考查的是解直角三角形的应用-坡度坡角问题，掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
19．
如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为弧AB的一个三等分点（靠近点B），D，E分别是OA，OB的中点，则图中阴影部分的面积为（ ）
如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为弧AB的一个三等分点（靠近点B），D，E分别是OA，OB的中点，则图中阴影部分的面积为（ ）| A． | $\frac{π+\sqrt{2}-1}{2}$cm2 | B． | $\frac{2}{3}$πcm2 | C． | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D． | $\frac{π+\sqrt{3}-1}{2}$cm2 |
20．
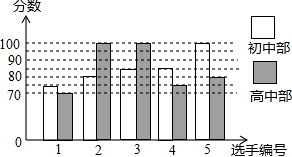某中学举行歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
求得初中代表队选手决赛成绩的平均数和方差：
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85，
${{S}_{1}}^{2}$=$\frac{1}{5}$[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70；
（1）根据图示填写表格：
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
某中学举行歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．求得初中代表队选手决赛成绩的平均数和方差：
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85，
${{S}_{1}}^{2}$=$\frac{1}{5}$[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70；
（1）根据图示填写表格：
| 平均数（分） | 中位数（分） | 众数（分） | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
（3）计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
如图，在Rt△ABC中，∠BAC=90°，∠B=60°，BC=16cm，AD是斜边BC上的高，垂足为D，BE=1cm，点M从点B出发沿BC方向以1cm/s的速度运动，点N从点E出发，与点M同时同方向以相同速度运动，点N到达点C时停止运动，设运动时间为t（s）．