题目内容
7.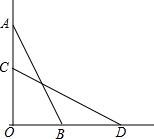 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)
分析 设梯子长度为xm,由OB=AB•cos∠ABO=$\frac{1}{2}$x、OD=CD•cos∠CDO=$\frac{\sqrt{2}}{2}$x,根据BD=OD-OB列方程求解可得.
解答 解:设梯子的长为xm.
在Rt△ABO中,∵cos∠ABO=$\frac{OB}{AB}$,
∴OB=AB•cos∠ABO=x•cos60°=$\frac{1}{2}$x,
在Rt△CDO中,∵cos∠CDO=$\frac{OD}{CD}$,
∴OD=CD•cos∠CDO=x•cos45°=$\frac{\sqrt{2}}{2}$x.
∵BD=OD-OB,
∴$\frac{\sqrt{2}}{2}$x-$\frac{1}{2}$x=1,
解得x=2$\sqrt{2}$+2.
故梯子的长是(2$\sqrt{2}$+2)米.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
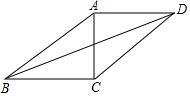 在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°,
在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°, 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
 如图,在△ABC中,DE是AC的垂直平分线,点D在BC上,△ABC的周长为20cm,△ABD的周长为12cm,则AE的长为4cm.
如图,在△ABC中,DE是AC的垂直平分线,点D在BC上,△ABC的周长为20cm,△ABD的周长为12cm,则AE的长为4cm. 如图,已知△ABC,∠BAC=90°,AB=6,AC=8.
如图,已知△ABC,∠BAC=90°,AB=6,AC=8. 如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.