题目内容
17. 如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
如图,⊙M经过原点O和点A(4,0)、点B(0,3),点P是⊙M上一点,并在x轴上方,则sin∠P=$\frac{4}{5}$.
分析 连接AB,根据圆周角定理得到AB是⊙M的直径,根据三角函数的定义即可得到结论.
解答  解:连接AB,
解:连接AB,
∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(4,0)、点B(0,3),
∴OA=4,OB=3,
∴AB=5,
∴sin∠P=sin∠B=$\frac{OA}{AB}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
2.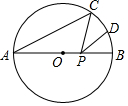 如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
 如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}-1$ |
19.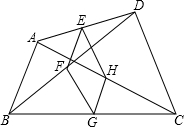 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
20.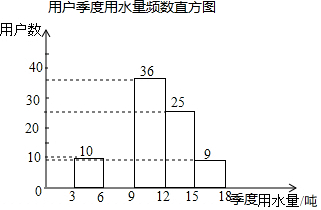 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
用户季度用水量频数分布表
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:用户季度用水量频数分布表
| 平均用水量(吨) | 频数 | 频率 |
| 3<x≤6 | 10 | 0.1 |
| 6<x≤9 | m | 0.2 |
| 9<x≤12 | 36 | 0.36 |
| 12<x≤15 | 25 | n |
| 15<x≤18 | 9 | 0.09 |
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
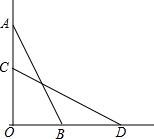 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)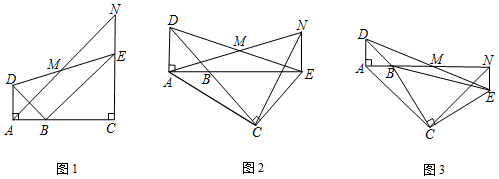
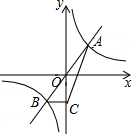 如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.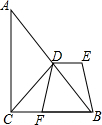 已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2.
已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2.