题目内容
17.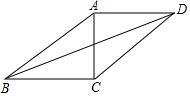 在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°,
在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°,(1)求BD的长.
(2)若点P从点B出发沿B-A-D的路线以2cm/s的速度向点D移动,同时点Q从点C出发沿C-D的路线以1cm/s的速度向点D移动,当一点到达C时,另一点也停止移动,当t取何值时,线段PQ将平行四边形ABCD的面积分为相等的两部分?
分析 (1)首先在Rt△ABC中,求出AC、BC,再在Rt△BOC中求出BO即可解决问题;
(2)易知当P在AB上,PA=CQ时,直线PQ将平行四边形ABCD的面积分成面积相等的两部分,由此列出方程即可解决问题.
解答 解: (1)如图设A 与BD交于点O.
(1)如图设A 与BD交于点O.
∵AC⊥BC,
∴∠ABC=30°,
∵AB=8,
∴AC=$\frac{1}{2}$AB=4.BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵四边形ABCD是平行四边形,
∴OA=OC=2,OB=OD,
在Rt△BOC中,OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{(4\sqrt{3})^{2}+{2}^{2}}$=2$\sqrt{13}$,
∴BD=4$\sqrt{13}$.
(2)易知当P在AB上,PA=CQ时,直线PQ将平行四边形ABCD的面积分成面积相等的两部分,
∴8-2t=t,
∴t=$\frac{8}{3}$,
∴t=$\frac{8}{3}$s时,直线PQ将平行四边形ABCD的面积分成面积相等的两部分.
点评 本题考查平行四边形的性质、勾股定理、直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程,属于中考常考题型.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.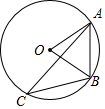 如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( )
如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( )
 如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( )
如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 60° |

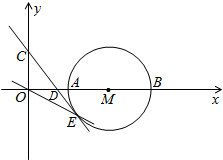 如图,点M(4,0),以点M为圆心,2为半径的圆与x轴交于点A、B,已知抛物线y=$\frac{1}{6}$x2+bx+c过点A和B,与y轴交于点C.
如图,点M(4,0),以点M为圆心,2为半径的圆与x轴交于点A、B,已知抛物线y=$\frac{1}{6}$x2+bx+c过点A和B,与y轴交于点C. 如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.
如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.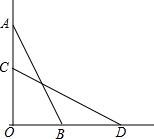 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号)