题目内容
19．
如图，已知△ABC，∠BAC=90°，AB=6，AC=8．（1）请用尺规过点A作一条线段与BC交于D，使其将△ABC分成两个相似的三角形（保留作图痕迹，不写作法）
（2）求AD的长．
分析 （1）过点A作AD⊥BC于D，利用相似三角形的判定方法可得到△ABD与△CAD相似；
（2）利用面积法计算AD的长．
解答 解：（1）如图，AD为所作．
（2）在Rt△ABC中，BC=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵$\frac{1}{2}$AD•BC=$\frac{1}{2}$AB•AC，
∴AD=$\frac{6×8}{10}$=4.8．
点评 本题考查了作图-相似变换、勾股定理、相似三角形的判定与性质以及三角形面积的计算；熟练掌握勾股定理和相似三角形的判定与性质是解决问题的关键．
练习册系列答案
相关题目
9．
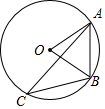如图，⊙O是△ABC的外接圆，点C、O在弦AB的同侧．若∠ACB=40°，则∠ABO的大小为（ ）
如图，⊙O是△ABC的外接圆，点C、O在弦AB的同侧．若∠ACB=40°，则∠ABO的大小为（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 60° |
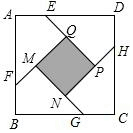如图，在边长为a（a＞2）的正方形各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，则正方形MNPQ的面积为2．
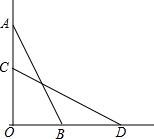如图，梯子斜靠在与地面垂直（垂足为O）的墙上，当梯子位于AB位置时，它与地面所成的角∠ABO=60°；当梯子底端向右滑动1m（即BD=1m）到达CD位置时，它与地面所成的角∠CDO=45°，求梯子的长（结果保留根号）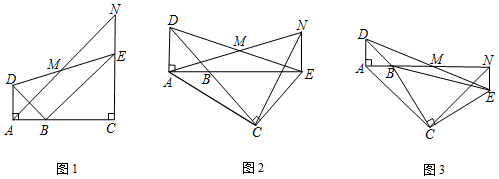
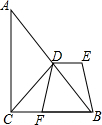已知：如图，△ABC中，∠ACB=90°，D为AB边中点，点F在BC边上，DE∥CF，且DE=CF．若DF=2，EB的长为2．