题目内容
11.已知:在?ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H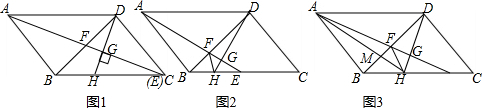
(1)如图1,若点E与点C重合,且AF=$\sqrt{5}$,求AD的长;
(2)如图2,连接FH,求证:∠AFB=∠HFB;
(3)如图3,连接AH交BF于M,当M为BF的中点时,请直接写出AF与FH的数量关系.
分析 (1)如图1中,利用等腰三角形的性质可得∠ABD=90°,利用平行四边形的性质可得F为BD中点,在Rt△ABF中,由勾股定理可求得BF,则可求得AB,在Rt△ABD中,再利用勾股定理可求得AD;
(2)如图2中,在AF上截取AK=HD,连接BK,可先证明△ABK≌△DBH,再证明△BFK≌△BFH,可证得结论;
(3)如图3中,延长FH、AB交于点N,作BK∥AH交FN于K,首先证明FA=FN,再证明FH=HK=KN,即可解决问题.
解答 (1)解:如图1中,∵AB=BD,∠BAD=45°,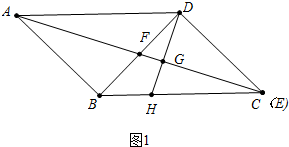
∴∠BDA=∠BAD=45°,
∴∠ABD=90°,
∵四边形ABCD是平行四边形,
∴E、C重合时BF=$\frac{1}{2}$BD=$\frac{1}{2}$AB,
在RT△ABF中,∵AF2=AB2+BF2,
∴($\sqrt{5}$)2=(2BF)2+BF2,
∴BF=1,AB=2,
在RT△ABD中,AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=2$\sqrt{2}$.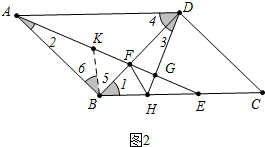
(2)证明:如图2中,在AF上截取AK=HD,连接BK,
∵∠AFD=∠ABF+∠2=∠FGD+∠3,∠ABF=∠FGD=90°,
∴∠2=∠3,
在ABK和△DBH中,
$\left\{\begin{array}{l}{AB=BD}\\{∠2=∠3}\\{AK=HD}\end{array}\right.$,
∴△ABK≌△DBH,
∴BK=BH,∠6=∠1,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠4=∠1=∠6=45°,
∴∠5=∠ABD-∠6=45°,
∴∠5=∠1,
在△FBK和△FBH中,
$\left\{\begin{array}{l}{BF=BF}\\{∠5=∠1}\\{BK=BH}\end{array}\right.$,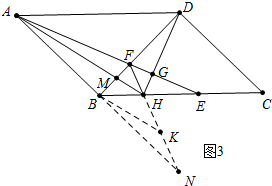
∴△FBK≌△FBH,
∴∠BFK=∠BFH.
(3)结论AF=3FH.
理由:如图3中,延长FH、AB交于点N,作BK∥AH交FN于K.
∵∠AFB+∠BAF=90°,∠BFN+∠N=90°,∠BFN=∠BFA,
∴∠FAB=∠N,
∴FA=FN,
∵FB⊥AN,
∴AB=BN,
∵BK∥AH,
∴HK=KN,
∵FM=BM,MH∥BK,
∴FH=HK,
∴FH=HK=FN.
∴FN=3FH,
∵AF=FN,
∴AF=3FH.
点评 本题考查四边形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.

| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
| A. | a<0 | B. | a>0 | C. | a≥0 | D. | 无法确定 |
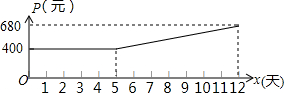 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.| 时间x(天) | 2 | 4 |
| 每天产量y(吨) | 24 | 28 |
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
| A. | 2 | B. | -2 | C. | 4 | D. | ±4 |

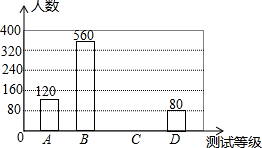 某区为了解2016年即将毕业的初中学生的心理状态,围绕“即将中考,你感觉自己的心理状态为:A优、B良、C中、D差(必须选且只选一项)”对全区各个学校随机抽取部分学生进行了问卷调查,在整理调查问卷后绘制成如图所示的不完整的条形统计图,其中选A的学生人数占所调查人数的15%,请你根据以上信息回答下列问题:
某区为了解2016年即将毕业的初中学生的心理状态,围绕“即将中考,你感觉自己的心理状态为:A优、B良、C中、D差(必须选且只选一项)”对全区各个学校随机抽取部分学生进行了问卷调查,在整理调查问卷后绘制成如图所示的不完整的条形统计图,其中选A的学生人数占所调查人数的15%,请你根据以上信息回答下列问题: