题目内容
16．（1）解方程：x2+4x-5=0（2）解不等式组：$\left\{\begin{array}{l}{\frac{1}{2}x-1≥1}\\{\frac{1}{2}x-1≤2}\end{array}\right.$．
分析 （1）依据因式分解法解一元二次方程的一般步骤：①移项使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解；
（2）先求出其中各不等式的解集，再求出这些解集的公共部分．
解答 解：（1）左边因式分解，得：（x-1）（x+5）=0，
∴x-1=0或x+5=0，
解得：x=1或x=-5；
（2）解不等式组：$\left\{\begin{array}{l}{\frac{1}{2}x-1≥1}&{①}\\{\frac{1}{2}x-1≤2}&{②}\end{array}\right.$，
解不等式①，得：x≥4，
解不等式②，得：x≤6，
∴不等式组的解集为：4≤x≤6．
点评 本题主要考查因式分解法解一元二次方程和解不等式组的能力，熟练掌握观察方程的特点选择合适方法和正确求出每个不等式的解集是解题关键．
练习册系列答案
相关题目
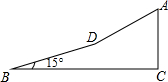如图，某校八年级（1）班学生利用寒假期间到郊区进行社会实践活动，活动之余，同学们准备攀登附近的一个小山坡，从B点出发，沿坡脚15°的坡面以5千米/时的速度行至D点，用了10分钟，然后沿坡比为1：$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点，用了5分钟，求小山坡的高（即AC的长度）（精确到0.01千米）（sin15°≈0.2588，cos15°≈0.9659，$\sqrt{3}$≈1.732）
如图，在一面靠墙的空地商用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．
1．
某艺术类学校进行绘画特长生的招生工作，每名考生需要参加“素描”“色彩”“速写”三个项目的测试，三个项目的满分均为100分，“素描”“色彩”“速写”按照4：4：2的比例计算得到选手最终成就，现有20名考生报名参加测试，测试结束后，考生的素描成绩如下（单位：分）：
88，85，90，99，86，68，94，98，78，97
96，93，89，94，89，85，80，95，89，77
请根据上述数据，解决下列问题：
（1）补全下面考生素描成绩的表格（每组数据含最小值不含最大值）和频数分布直方图；
（2）如表为甲、乙两名选手比赛成绩的记录表，现要在甲、乙二人中录取一名，请通过计算得出谁最终被录取．
某艺术类学校进行绘画特长生的招生工作，每名考生需要参加“素描”“色彩”“速写”三个项目的测试，三个项目的满分均为100分，“素描”“色彩”“速写”按照4：4：2的比例计算得到选手最终成就，现有20名考生报名参加测试，测试结束后，考生的素描成绩如下（单位：分）：88，85，90，99，86，68，94，98，78，97
96，93，89，94，89，85，80，95，89，77
请根据上述数据，解决下列问题：
（1）补全下面考生素描成绩的表格（每组数据含最小值不含最大值）和频数分布直方图；
| 分组 | 人数（频数） |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
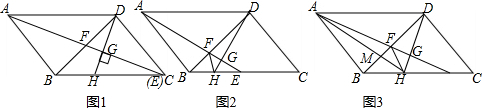
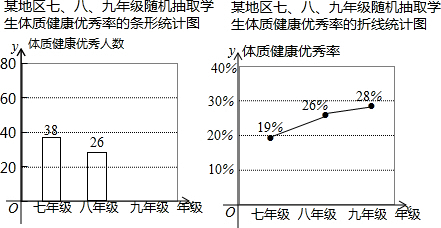
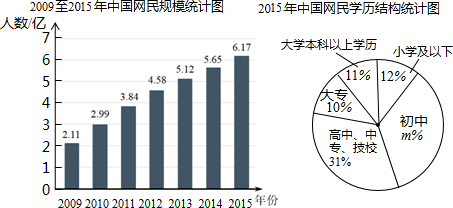
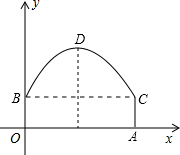如图，东湖隧道的截面由抛物线和长方形构成，长方形的长OA为12m，宽OB为4m，隧道顶端D到路面的距离为10m，建立如图所示的直角坐标系