题目内容
3．解方程：（1）x2-3x+2=0；
（2）$\frac{3}{x}-\frac{1}{x+2}=0$．
分析 （1）根据因式分解法解一元二次方程的步骤：①移项使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零得到两个一元一次方程；④解这两个一元一次方程，即可得答案；
（2）依据解分式方程的步骤：①去分母；②求出整式方程的解；③检验；④得出结论．
解答 解：（1）方程左边因式分解，得：（x-1）（x-2）=0，
∴x-1=0或x-2=0，
解得：x=1或x=2；
（2）去分母，得：3（x+2）-x=0，
去括号，得：3x+6-x=0，
移项、合并，得：2x=-6，
系数化为1，得：x=-3，
经检验：x=-3是原分式方程的解，
故该分式方程的解为x=-3．
点评 本题主要考查解分式方程和一元二次方程的能力，熟练掌握解方程的转化思想：分式方程转化为整式方程、一元二次方程因式分解转化为两个一元一次方程是解题的关键．
练习册系列答案
相关题目
8．
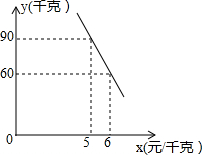某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．
（1）根据题意，填写如表：
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．（1）根据题意，填写如表：
| 蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
| 所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
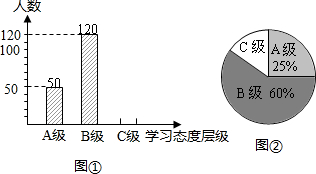某地教育部门对九年级学生的“学习态度”进行了一次抽样调查，把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣，要求被调查的学生从A、B、C三项中必选且只能选择一项，结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：