题目内容
4．
（1）先化简，再求值：2x（x-y）-（x-y）2，其中$x=\sqrt{2}，y=\sqrt{3}$（2）如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），请画出△ABC绕点C按逆时针旋转90°后得到的△A′BC，并写出A的对应点A′的坐标（-3，-3）．
分析 （1）原式利用单项式乘以多项式，以及完全平方公式化简，去括号合并得到最简结果，把x与y的值代入计算即可求出值；
（2）作出△ABC绕点C按逆时针旋转90°后得到的△A′B′C，找出A′坐标即可．
解答 解：（1）原式=2x2-2xy-x2+2xy-y2=x2-y2，
当x=$\sqrt{2}$，y=$\sqrt{3}$时，原式=2-3=-1；
（2）画出△ABC绕点C按逆时针旋转90°后得到的△A′B′C，如图所示：
则A的对应点A′的坐标为（-3，-3）．
故答案为：（-3，-3）
点评 此题考查了作图-旋转变换，以及整式的混合运算-化简求值，熟练掌握旋转的性质是解本题的关键．
练习册系列答案
相关题目
如图，在?ABCD中，对角线AC、BD相交于点O，点E是CD的中点，BC=12，则OE的长为6．
如图，直线y=x-4与x轴、y轴分别交于M、N两点，⊙O的半径为2，将⊙O以每秒1个单位的速度向右作平移运动，当移动时间4-2$\sqrt{2}$或4+2$\sqrt{2}$秒时，直线MN恰好与圆相切．
9．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{（-a+b）^2}{（a-b）^2}$=1 | B． | $\frac{-a-1}{-a^2+8}$=$\frac{a-1}{a^2+8}$ | ||
| C． | $\frac{x^2+y^2}{x+y}$=x+y | D． | $\frac{0.5+2y}{-0.1+x}$=$\frac{5+2y}{1+x}$ |
如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为32，则OE的长等于（ ）
13．
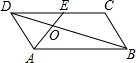如图，在?ABCD中，E为CD的中点，AE交BD于点O，S△DCE=12，则S△AOD等于（ ）
如图，在?ABCD中，E为CD的中点，AE交BD于点O，S△DCE=12，则S△AOD等于（ ）| A． | 24 | B． | 36 | C． | 48 | D． | 60 |
如图，点C是线段AB上一点，点M、N、P分别是线段AC，BC，AB的中点．