题目内容
3. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )| A. | 4 | B. | 8 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 先利用直角三角形斜边中线性质求出AB,再在RT△ABF中,利用30角所对的直角边等于斜边的一半,求出AF即可解决问题.
解答  解:在RT△ABF中,∵∠AFB=90°,AD=DB,DF=4,
解:在RT△ABF中,∵∠AFB=90°,AD=DB,DF=4,
∴AB=2DF=8,
∵AD=DB,AE=EC,
∴DE∥BC,
∴∠ADE=∠ABF=30°,
∴AF=$\frac{1}{2}$AB=4,
∴BF=$\sqrt{A{B}^{2}-A{F}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
故选D.
点评 本题考查三角形中位线性质、含30度角的直角三角形性质、直角三角形斜边中线性质、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.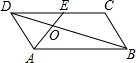 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DCE=12,则S△AOD等于( )| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
13.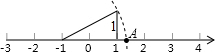 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )
 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{5}$-1 | D. | 1-$\sqrt{5}$ |
 如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.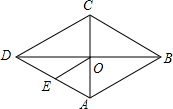 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( ) 如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为2.
如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为2.