题目内容
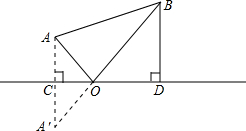 如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.
如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.考点:轴对称-最短路线问题
专题:
分析:根据题意构造直角三角形,进而得出AF的长,再求出A′B的长,即可得出答案.
解答: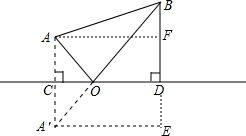 解:如图所示:过点A作AF⊥BD于点F,过点A′作A′E⊥BD延长线于点E,
解:如图所示:过点A作AF⊥BD于点F,过点A′作A′E⊥BD延长线于点E,
由题意可得:A点关于CD的对称点为A′,连接A′B交CD于点O,此时AO+BO最小,
∵AC=1km,BD=3km,
∴BF=2km,DE=1km,
∵AB2=13km,
∴AF=
=3(km),
在Rt△BA′E中
A′E2+BE2=A′B2,
即32+42=A′B2,
解得:A′B=5,
则AO+BO=5(km),
故铺设水管的总费用W=5×3000=15000(元).
 解:如图所示:过点A作AF⊥BD于点F,过点A′作A′E⊥BD延长线于点E,
解:如图所示:过点A作AF⊥BD于点F,过点A′作A′E⊥BD延长线于点E,由题意可得:A点关于CD的对称点为A′,连接A′B交CD于点O,此时AO+BO最小,
∵AC=1km,BD=3km,
∴BF=2km,DE=1km,
∵AB2=13km,
∴AF=
| 13-22 |
在Rt△BA′E中
A′E2+BE2=A′B2,
即32+42=A′B2,
解得:A′B=5,
则AO+BO=5(km),
故铺设水管的总费用W=5×3000=15000(元).
点评:此题主要考查了轴对称求最短路径,解这类问题的关键是将实际问题抽象或转化为几何模型,把两条线段的和转化为一条线段,运用三角形三边关系解决.

练习册系列答案
相关题目
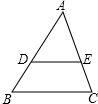 如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=
如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC= 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y= 已知AB=6cm,AD=10cm,△ABE和△ADF的面积各是长方形ABCD面积的
已知AB=6cm,AD=10cm,△ABE和△ADF的面积各是长方形ABCD面积的