题目内容
17.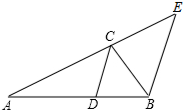 如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.
如图,已知△ABC的角平分线CD交AB于D点,过点B作BE∥CD交AC的延长线于点E.(1)求证:△BCE是等腰三角形;
(2)若AD=$\sqrt{3}$,BD=$\sqrt{2}$,求$\frac{AC}{CB}$的值.
分析 (1)根据CD平分∠ACB,可知∠ACD=∠BCD;由BE∥CD,可求出△BCE是等腰三角形,CB=CE即可;
(2)根据平行线分线段成比例定理以及BC=CE,即可得出结果.
解答 (1)证明:∵CD平分∠ACB,
∴∠ACD=∠BCD.
又∵BE∥CD,
∴∠CBE=∠BCD,∠CEB=∠ACD.
∵∠ACD=∠BCD,
∴∠CBE=∠CEB.
∴CB=CE,即△BCE是等腰三角形.
(2)解:∵BE∥CD,
根据平行线分线段成比例定理得:$\frac{AC}{CE}=\frac{AD}{BD}$,
∵CB=CE,
∴$\frac{AC}{CB}=\frac{AD}{BD}$=$\frac{\sqrt{3}}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$.
点评 本题主要考查了平行线分线段成比例定理、等腰三角形的判定和角平分线定理的证明;熟练掌握平行线分线段成比例定理,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.下列标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230kW•h的部分为第一档,按每千瓦时0.49元收费;超过230千kW•h且不超过400kW•h的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400kW•h的部分为第三档,超过的部分按每千瓦时0.79元收费.
(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:
(2)设一户家庭某月用电量为xkW•h,写出该户此月应缴电费y(元)与用电量x(kW•h)之间的函数关系式.
(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:
| 4月份总用电量/kW•h | 电费/元 | |
| 小刚 | 200 | 98 |
| 小丽 | 320 | 161.3 |
| 小红 | 450 | 244 |
 如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )
如图是由5个大小相同的小正方体摆成的立体图形,则从正面看得到的平面图形是( )



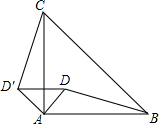 如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.
如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置,则∠ADD′=45°.