题目内容
已知abc=2,a+b+c=6,a2+b2+c2=18,求
+
+
的值.
| 1 |
| ab+c-5 |
| 1 |
| bc+a-5 |
| 1 |
| ac+b-5 |
考点:分式的化简求值
专题:
分析:由a+b+c=2,两边平方得a2+b2+c2+2ab+2bc+2ac=36,求出ab+bc+ac=-6,原式化为
,整体代入求值即可.
| -1 |
| abc-ac-bc+c-ab+a+b-1 |
解答:解:由a+b+c=2,两边平方,得a2+b2+c2+2ab+2bc+2ac=36,
将a2+b2+c2=18代入,得ab+bc+ac=-6,
由a+b+c=6得,c-5=1-a-b,
∴ab+c-5=ab+1-a-b=(a-1)(b-1),
同理bc+a-5=(b-1)(c-1),
ac+b-5=(a-1)(b-1),
∴原式=
+
+
=
=
=
=-
.
将a2+b2+c2=18代入,得ab+bc+ac=-6,
由a+b+c=6得,c-5=1-a-b,
∴ab+c-5=ab+1-a-b=(a-1)(b-1),
同理bc+a-5=(b-1)(c-1),
ac+b-5=(a-1)(b-1),
∴原式=
| 1 |
| (a-1)(b-1) |
| 1 |
| (b-1)(c-1) |
| 1 |
| (c-1)(a-1) |
=
| c-1+a-1+b-1 |
| (a-1)(b-1)(c-1) |
=
| -1 |
| abc-ac-bc+c-ab+a+b-1 |
=
| -1 |
| 2+6+2-1 |
=-
| 1 |
| 9 |
点评:本题考查了分式的化简求值,要灵活进行转化,同时要熟悉整体思想.

练习册系列答案
相关题目
已知方程组
,那么x的值是( )
|
| A、1 | B、2 | C、-1 | D、-2 |
在多边形一个外角等于60°,则这个多边形的边数为( )
| A、3 | B、4 | C、6 | D、8 |
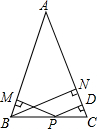 如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN.
如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN. 如图是某几何体的二视图,求它的表面积和体积.
如图是某几何体的二视图,求它的表面积和体积. 如图,在⊙O中,D,E分别是半径OA,OB的中点,点C在圆上,CD=CE.求证:
如图,在⊙O中,D,E分别是半径OA,OB的中点,点C在圆上,CD=CE.求证: