Question

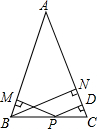如图，在△ABC中，AB=AC，P为BC上一点，PD⊥AC于点D，PM⊥AB于点M，BN为高，求证：PD+PM=BN．

Answer 1

考点：等腰三角形的性质

专题：作图题

分析：连接AP，根据等腰三角形的性质可表示出△ABC与△ABP、△APC的关系，同时可表示出S_△ABC=

1

2

AB×BN，从而可得到PD+PM=BN．

解答：证明：连接AP．
∵AB=AC，
∴S_△ABC=S_△ABP+S_△ACP=

1

2

AB×PM+

1

2

AC×PD=

1

2

×AB×（PD+PM），
∵S_△ABC=

1

2

AB×BN，
∴PD+PM=BN．

点评：本题主要考查了等腰三角形的性质及三角形面积的综合运用，此题的关键是利用面积公式将所求联系在一起，难度适中．