题目内容

7．解方程组：
①$\left\{\begin{array}{l}{2（x-1）-y=6}\\{x=y-1}\end{array}\right.$                      
②$\left\{\begin{array}{l}4x-3y=11，\;\\ 2x+y=13\;.\end{array}\right.$．

分析 ①方程组利用代入消元法求出解即可；
②方程组利用加减消元法求出解即可．

解答 解：①$\left\{\begin{array}{l}{2x-y=8①}\\{x=y-1②}\end{array}\right.$，
把②代入①得：2y-2-y=8，
解得：y=10，
把y=10代入②得：x=9，
则方程组的解为$\left\{\begin{array}{l}{x=9}\\{y=10}\end{array}\right.$；
②$\left\{\begin{array}{l}{4x-3y=11①}\\{2x+y=13②}\end{array}\right.$，
①+②×3得：10x=50，
解得：x=5，
把x=5代入②得：y=3，
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$．

点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案
相关题目
8．如图，△ABC∽△BDC，BC=$\sqrt{6}$，AC=3，则CD的长为（　　）
A．1B．2C．3D．4
18．（1）（1-π）×$\root{3}{27}$-（$\frac{1}{7}$）-1+|-2|
（2）先化简，再求值：$\frac{{a}^{2}-2a}{{a}^{2}-1}$÷（a-1-$\frac{2a-1}{a+1}$，其中a=3．
15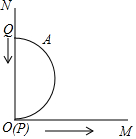．如图，己知射线OM与射线ON互相垂直，A是直径PQ为2cm的半圆铁片上一点，且弧AQ的度数为60°，（即弧AQ所对的圆心角为60°）动点P从点O沿射线OM开始滑动，同时动点Q在ON上滑动，当点Q滑至点O停止时，点A所经过的路程是（　　）
A．3B．3-$\sqrt{3}$C．3+$\sqrt{3}$D．6-2$\sqrt{3}$
2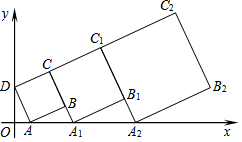．在平面直角坐标系中，正方形ABCD的位置如下图所示，点A的坐标为（1，0），点D的坐标为（0，3）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2012个正方形的面积为（　　）
A．$\sqrt{10}$×（$\frac{4}{3}$）4022B．10×（$\frac{4}{3}$）4022C．5×（$\frac{4}{3}$）4022D．10×（$\frac{4}{3}$）4023
12．计算：（-$\frac{3}{2}$）2÷（-$\frac{1}{2}$）2×（1$\frac{1}{3}$）2-（-4）2-42．
19．如图1，在边长为4的正△ABC中，点P以每秒1cm的速度从点A出发，沿折线AB-BC运动，到点C停止．过点P作PD⊥AC，垂足为D，PD的长度y（cm）与点P的运动时间x（秒）的函数图象如图2所示．当点P运动5.5秒时，PD的长是（　　）
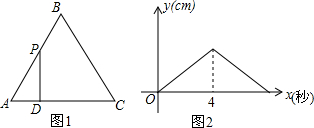
A．$\frac{5\sqrt{3}}{4}$cmB．$\frac{5\sqrt{3}}{2}$cmC．2$\sqrt{3}$cmD．3$\sqrt{3}$cm
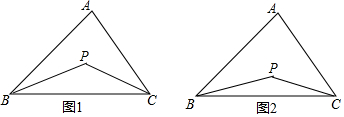16．【提出问题】已知如图1，P是∠ABC、∠ACB的角平分线的交点，你能找到∠P、∠A的关系吗？
【分析问题】在解决这个问题时，某小组同学是这样做的：
先赋予∠A几个特殊值：
当∠A=80°时，计算出∠P=130°；
当∠A=40°时，计算出∠P=110°；
当∠A=100°时，计算出∠P=140°；
…由以上特例猜想∠P与∠A的关系为：∠P=90°+$\frac{1}{2}$∠A．再证明这一结论：
证明：∵点P是∠ABC、∠ACB的角平分线的交点．
∴∠PBC=$\frac{1}{2}$∠ABC；∠PCB=$\frac{1}{2}$∠ACB
∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
又∵∠A+（∠ABC+∠ACB）=180°
∴∠ABC+∠ACB=180°-∠A
∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
=$\frac{1}{2}$（180°-∠A）
∴∠P=180°-（∠PBC+∠PCB）
=180°-$\frac{1}{2}$（180°-∠A）
=90°+$\frac{1}{2}$∠A
【解决问题】请运用以上解决问题的“思想方法”解决下面的几个问题：
（1）如图2，若点P时∠ABC、∠ACB的三等分线的交点，即∠PBC=$\frac{1}{3}$∠ABC，∠PCB=$\frac{1}{3}$∠ACB，猜测∠P与∠A的关系为∠P=$\frac{1}{3}$∠A+$\frac{2}{3}$×180°，证明你的结论．
（2）若点P时∠ABC、∠ACB的四等分线的交点，即∠PBC=$\frac{1}{4}$∠ABC，∠PCB=$\frac{1}{4}$∠ACB，则∠P与∠A的关系为∠P=$\frac{1}{4}$∠A+$\frac{3}{4}$×180°．（直接写出答案，不需要证明）
（3）若点P时∠ABC、∠ACB的n等分线的交点，即∠PBC=$\frac{1}{n}$∠ABC，∠PCB=$\frac{1}{n}$∠ACB，则∠P与∠A的关系为$\frac{n-1}{n}$•180°+$\frac{1}{n}$∠A．（直接写出答案，不需要证明）
17．解方程组：$\left\{\begin{array}{l}{x+2z=3}\\{2y+z=7}\\{2x-y-z=-5}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网