题目内容
15.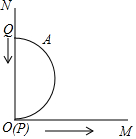 如图,己知射线OM与射线ON互相垂直,A是直径PQ为2cm的半圆铁片上一点,且弧AQ的度数为60°,(即弧AQ所对的圆心角为60°)动点P从点O沿射线OM开始滑动,同时动点Q在ON上滑动,当点Q滑至点O停止时,点A所经过的路程是( )
如图,己知射线OM与射线ON互相垂直,A是直径PQ为2cm的半圆铁片上一点,且弧AQ的度数为60°,(即弧AQ所对的圆心角为60°)动点P从点O沿射线OM开始滑动,同时动点Q在ON上滑动,当点Q滑至点O停止时,点A所经过的路程是( )| A. | 3 | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 6-2$\sqrt{3}$ |
分析 由题意,PQ滑动过程中,PQ=2,∠QOA=30°,所以点A在射线OA上运动,起始位置时OA=$\sqrt{3}$,当P′Q′的中点在直线OA上时,OA′最长,此时OA′=2,TC AA′=2-$\sqrt{3}$,当点Q″与O重合时,OA″最小,此时OA″=1,所以点A的运动路径为A→A′→A→A″,由此求出AA′+A′A″即可解决问题.
解答 解:如图,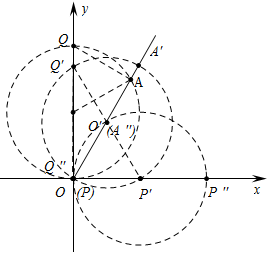
由题意,PQ滑动过程中,PQ=2,∠QOA=30°,所以点A在射线OA上运动,
起始位置时OA=$\sqrt{3}$,当P′Q′的中点在直线OA上时,OA′最长,此时OA′=2,
∴AA′=2-$\sqrt{3}$,
当点Q″与O重合时,OA″最小,此时OA″=1,
点A的运动路径为A→A′→A→A″,
∴点A所经过的路程=2-$\sqrt{3}$+(2-1)=3-$\sqrt{3}$,
故选B.
点评 本题考查轨迹,圆心角、弦、弧之间的关系等知识,解题的关键是发现∠AOQ=30°,求出OA的最大值以及最小值,题目比较难,所以中考选择题中的压轴题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各不相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
6.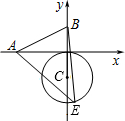 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )| A. | 2+$\frac{\sqrt{5}}{2}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 3+$\frac{\sqrt{3}}{2}$ | D. | 4+$\frac{\sqrt{3}}{2}$ |
20.下列条件中,不能判定三角形全等的是( )
| A. | 三条边对应相等 | B. | 两边和其中一角对应相等 | ||
| C. | 两边和夹角对应相等 | D. | 两角和它们的夹边对应相等 |
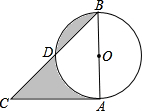 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.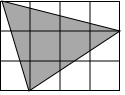 如图由12个相同小正方形组成一个长方形.
如图由12个相同小正方形组成一个长方形.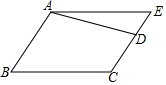 如图,已知AB∥CD,过点A作射线AE,交CD的延长线于点E,试问:AE与BC一定平行吗?并说明你的理由.
如图,已知AB∥CD,过点A作射线AE,交CD的延长线于点E,试问:AE与BC一定平行吗?并说明你的理由.