题目内容
15.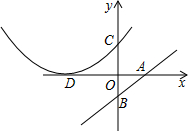 如图,直线AB的函数表达式为y=$\frac{m}{4}$x-m(m≠0,m为常数),点A、B分别在x轴、y轴上,tan∠OAB=$\frac{3}{4}$,点B关于x轴的对称点为点C,以D(-6,0)为顶点的抛物线经过点C.
如图,直线AB的函数表达式为y=$\frac{m}{4}$x-m(m≠0,m为常数),点A、B分别在x轴、y轴上,tan∠OAB=$\frac{3}{4}$,点B关于x轴的对称点为点C,以D(-6,0)为顶点的抛物线经过点C.(1)求抛物线的解析式;
(2)在x轴上有点P,以点的C,O,P为顶点的△COP与△ABO相似,请求出点P的坐标;
(3)动点Q在抛物线上,当点Q到直线AB的距离最小时,求出点Q的坐标及最小距离.
分析 (1)首先求出A、B、C坐标,根据顶点坐标,设抛物线的解析式为y=a(x+6)2,把C(0,3)代入求出a即可.
(2)分两种情形讨论,①当点P在原点O左边,满足$\frac{OP}{OA}$=$\frac{OC}{OB}$时,△POC∽△AOB,②当点P在原点O左边,满足$\frac{OP}{OB}$=$\frac{OC}{OA}$时,△POC∽△BOA,
求出P1,P2后,再求出P3、P4即可.
(3)如图2中,设Q[n,$\frac{1}{12}$(n+6)2],作QN⊥AB于N,QM∥BC交AB于M,则M(n,$\frac{3}{4}$n-3),首先说明△MQN的三个内角是固定不变的,欲求QN的最小值,只要求出QM的最小值即可,再根据QN的最小值=QM•cos∠MQN=QM•cos∠OAB计算即可.
解答 解:(1)∵直线AB的函数表达式为y=$\frac{m}{4}$x-m,
∴A(4,0),B(0,-m),
在Rt△AOB中,∵OA=4,tan∠OAB=$\frac{3}{4}$=$\frac{OB}{OA}$,
∴OB=3,m=3,
∴B(0,-3),
∵B、C关于x轴对称,
∴C(0,3),
∵抛物线的顶点为(-6,0),
∴可以假设抛物线的解析式为y=a(x+6)2,把C(0,3)代入得a=$\frac{1}{12}$,
∴抛物线的解析式为y=$\frac{1}{12}$(x+6)2.
(2)如图1中,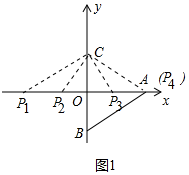
①当点P在原点O左边,满足$\frac{OP}{OA}$=$\frac{OC}{OB}$时,△POC∽△AOB,
∴$\frac{OP}{4}$=$\frac{3}{3}$,
∴OP=4,可得P1(-4,0).
②当点P在原点O左边,满足$\frac{OP}{OB}$=$\frac{OC}{OA}$时,△POC∽△BOA,
∴$\frac{OP}{3}$=$\frac{3}{4}$,
∴OP=$\frac{9}{4}$,可得P2(-$\frac{9}{4}$,0).
③根据对称性可知当P3($\frac{9}{4}$,0),P4(4,0)时,也满足条件.
综上所述,满足条件的点P坐标为(-4,0)或(-$\frac{9}{4}$,0)或(4,0)或($\frac{9}{4}$,0).
(3)如图2中,设Q[n,$\frac{1}{12}$(n+6)2],作QN⊥AB于N,QM∥BC交AB于M,则M(n,$\frac{3}{4}$n-3),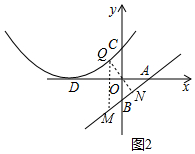
∵∠MQN+∠AMQ=90°,∠AMQ+∠BAO=90°,
∴∠MQN=∠BAO,
∴△MQN的三个内角是固定不变的,
∴欲求QN的最小值,只要求出QM的最小值即可,
∵QM=$\frac{1}{12}$(n+6)2-($\frac{3}{4}$n-3)=$\frac{1}{12}$(n+$\frac{3}{2}$)2+$\frac{93}{16}$,
∵$\frac{1}{12}$>0,
∴n=-$\frac{3}{2}$时,QM的最小值为$\frac{93}{16}$,
∴QN的最小值=QM•cos∠MQN=QM•cos∠OAB=$\frac{93}{16}$×$\frac{4}{5}$=$\frac{93}{20}$.
点评 本题考查二次函数的综合题、相似三角形的判定和性质、锐角三角函数、勾股定理、待定系数法等知识,解题的关键是灵活运用首先知识,学会用转化的思想思考问题,学会构建二次函数解决最值问题,第三个问题的关键是把求QN的最小值,转化为求QM的最小值,属于中考压轴题.

 如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,
如图,AB、CD为⊙O的两条弦,已知AB⊥CD于点E,OF⊥AB于点F,已知AC=4$\sqrt{5}$,BD=6$\sqrt{5}$,EF=1,则OE的长是( )
| A. | 3 | B. | 4 | C. | $\sqrt{17}$ | D. | 4$\sqrt{5}$ |
| A. | 画一个三角形其内角和为361° | |
| B. | 任意做一个矩形,其对角线相等 | |
| C. | 任取一个实数,其相反数之和为0 | |
| D. | 外观相同的10件同种产品中有2件是不合格产品,现从中抽取一件恰为合格品 |
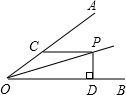 如图,∠AOP=∠OPC=15°,PC∥DO,PD⊥OB,若OC=8,则PD等于4.
如图,∠AOP=∠OPC=15°,PC∥DO,PD⊥OB,若OC=8,则PD等于4. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为8.
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为8.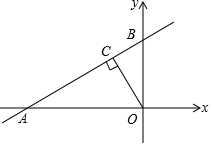 如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).
如图,直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$与x轴、y轴分别交于A,B两点,过点O作OC⊥AB于点C,点P是OA上的动点,若使△PAC为等腰三角形,则点P的坐标是(2$\sqrt{3}$-4,0)或(-2,0).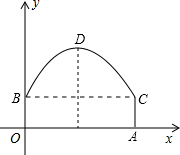 如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.
如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.