题目内容
11．
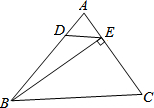如图，锐角△ABC中，BE⊥AC，∠ADE=∠C，记△ADE的面积S1，△ABC的面积S2，则$\frac{S_1}{S_2}$=（ ）| A． | sin2A | B． | cos2A | C． | tan2A | D． | $\frac{1}{{{{tan}^2}A}}$ |
分析 根据相似三角形的性质和三角形函数即可得到结论．
解答 解：∵∠ADE=∠C，∠A=∠A，
∴△ADE∽△ACB，
∴$\frac{{S}_{1}}{{S}_{2}}$=（$\frac{AE}{AB}$）2，
∵BE⊥AC，
∴cosA=$\frac{AE}{AB}$，
∴$\frac{S_1}{S_2}$=（$\frac{AE}{AB}$）2=cos2A，
故选B．
点评 本题考查了相似三角形的判定和性质，三角函数，熟练掌握相似三角形的判定和性质定理是解题的关键．
练习册系列答案
相关题目
1．已知：$\sqrt{\frac{1-m}{{m}^{2}}}$=$\frac{\sqrt{1-m}}{m}$，则m的取值范围是（ ）
| A． | m＜0 | B． | m≥0 | C． | 0≤m≤1 | D． | 0＜m≤1 |
19．若某一元二次方程的两个根是3和-5，则这个方程是（ ）
| A． | x2-2x-15=0 | B． | x2-2x+15=0 | C． | x2+2x-15=0 | D． | x2+2x+15=0 |