题目内容
20.在正方形ABCD中,O是对角线的交点,AB=12,则△OAB的周长为$12\sqrt{2}+12$.分析 根据正方形的性质得出△AOB是等腰直角三角形,得出OA=OB=$\frac{\sqrt{2}}{2}×12=6\sqrt{2}$.
解答 解:∵正方形ABCD中,O是对角线的交点,AB=12,
∴OA=OB=$\frac{\sqrt{2}}{2}×12=6\sqrt{2}$,
△OAB的周长为$12\sqrt{2}+12$.
故答案为:$12\sqrt{2}+12$.
点评 此题考查正方形的性质,关键是根据正方形的性质得出△AOB是等腰直角三角形.

练习册系列答案
相关题目
10.下列变形是因式分解的是( )
| A. | x(x+1)=x2+x | B. | x2+2x+1=(x+1)2 | C. | x2+xy-3=x(x+y)-3 | D. | x2+6x+4=(x+3)2-5 |
11.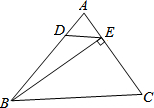 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )| A. | sin2A | B. | cos2A | C. | tan2A | D. | $\frac{1}{{{{tan}^2}A}}$ |
8.长沙地铁2号线于2013年12月30日试通车,规划总长约210000米,用科学记数法表示这个总长为( )
| A. | 2.1×105米 | B. | 2.1×106米 | C. | 0.21×106米 | D. | 21×104米 |
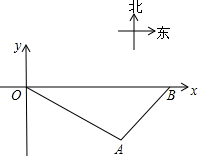 一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.
一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.