题目内容
19．若某一元二次方程的两个根是3和-5，则这个方程是（ ）| A． | x2-2x-15=0 | B． | x2-2x+15=0 | C． | x2+2x-15=0 | D． | x2+2x+15=0 |
分析 先计算3和-5的和与积，然后根据根与系数的关系写出满足条件的一元二次方程即可．
解答 解：∵3+（-5）=-2，
3×（-5）=-15，
∴以3和-5为根的一元二次方程可为x2+2x-15=0．
故选：C．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
10．下列变形是因式分解的是（ ）
| A． | x（x+1）=x2+x | B． | x2+2x+1=（x+1）2 | C． | x2+xy-3=x（x+y）-3 | D． | x2+6x+4=（x+3）2-5 |
7．在函数$y=\sqrt{3-x}+\frac{1}{{\sqrt{2x-1}}}$中，自变量x的取值范围是（ ）
| A． | $\frac{1}{2}＜x≤3$ | B． | $\frac{1}{2}≤x≤3$ | C． | x≤3且$x≠\frac{1}{2}$ | D． | $\frac{1}{2}＜x＜3$ |
11．
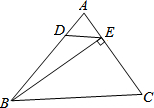如图，锐角△ABC中，BE⊥AC，∠ADE=∠C，记△ADE的面积S1，△ABC的面积S2，则$\frac{S_1}{S_2}$=（ ）
如图，锐角△ABC中，BE⊥AC，∠ADE=∠C，记△ADE的面积S1，△ABC的面积S2，则$\frac{S_1}{S_2}$=（ ）| A． | sin2A | B． | cos2A | C． | tan2A | D． | $\frac{1}{{{{tan}^2}A}}$ |
8．长沙地铁2号线于2013年12月30日试通车，规划总长约210000米，用科学记数法表示这个总长为（ ）
| A． | 2.1×105米 | B． | 2.1×106米 | C． | 0.21×106米 | D． | 21×104米 |