题目内容
1.已知:$\sqrt{\frac{1-m}{{m}^{2}}}$=$\frac{\sqrt{1-m}}{m}$,则m的取值范围是( )| A. | m<0 | B. | m≥0 | C. | 0≤m≤1 | D. | 0<m≤1 |
分析 直接利用二次根式的性质得出1-m≥0,m>0,进而得出答案.
解答 解:∵$\sqrt{\frac{1-m}{{m}^{2}}}$=$\frac{\sqrt{1-m}}{m}$,
∴1-m≥0,m>0,
解得:0<m≤1.
故选:D.
点评 此题主要考查了二次根式的乘除法,正确掌握二次根式的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.关于x的一元二次方程x2-mx+2m-1=0的两个实数根分别是x1,x2,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=7,则(x1-x2)2的值为( )
| A. | 1 | B. | 12 | C. | 13 | D. | 25 |
13.下列说法中正确的是( )
| A. | “打开电视,正在播放《自然传奇》”是必然事件 | |
| B. | 想了解某种饮料中含色素的情况,应进行全面调查 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 对报考空飞班的每个学生的身体情况必须进行全面调查 |
10.下列变形是因式分解的是( )
| A. | x(x+1)=x2+x | B. | x2+2x+1=(x+1)2 | C. | x2+xy-3=x(x+y)-3 | D. | x2+6x+4=(x+3)2-5 |
11.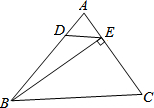 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )| A. | sin2A | B. | cos2A | C. | tan2A | D. | $\frac{1}{{{{tan}^2}A}}$ |
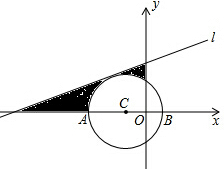 已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$
已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$