题目内容
1.已知a,b,c是△ABC的三边长,且满足关系式(c2-a2-b2)2+|a-b|=0,则△ABC的形状为等腰直角三角形.分析 根据绝对值和偶次方的非负性求出a=b,根据勾股定理的逆定理判断即可.
解答 解:因为(c2-a2-b2)2+|a-b|=0,
可得:a=b,c2=a2+b2,
所以△ABC的形状为等腰直角三角形.
故答案为:等腰直角三角形.
点评 本题考查了绝对值的性质,偶次方,勾股定理的逆定理的应用,关键是求出a2+b2=c2.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
11.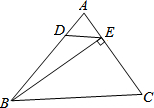 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )| A. | sin2A | B. | cos2A | C. | tan2A | D. | $\frac{1}{{{{tan}^2}A}}$ |
6.已知四个命题:①如果一个数的相反数等于它本身,则这个数是0②一个数的倒数等于它本身,则这个数是1③一个数的算术平方根等于它本身,则这个数是1或0④如果一个数的绝对值等于它本身,则这个数是正数,其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列说法正确的是( )
| A. | 定理不一定是真命题 | B. | 真命题不一定正确 | ||
| C. | 假命题不一定错误 | D. | 基本事实一定是真命题 |
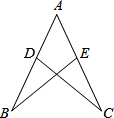 如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.
如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.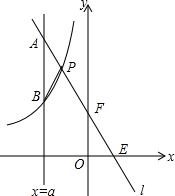 如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.