题目内容
2.化简:1-$\frac{2a+b}{a+2b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=1-$\frac{2a+b}{a+2b}$•$\frac{(a+2b)^{2}}{(a+b)(a-b)}$
=1-$\frac{(2a+b)(a+2b)}{(a+b)(a-b)}$
=$\frac{{a}^{2}-{b}^{2}-2{a}^{2}-5ab-2{b}^{2}}{{a}^{2}-{b}^{2}}$
=$\frac{-{a}^{2}-3{b}^{2}+5ab}{{a}^{2}-{b}^{2}}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17. 如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
 如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )| A. | 只有三角形 | |
| B. | 只有三角形和四边形 | |
| C. | 只有三角形,四边形和五边形 | |
| D. | 只有三角形,四边形,五边形和六边形 |
14.在Rt△ABC中,∠C=90°,若tan$\frac{B}{2}$=$\frac{\sqrt{3}}{3}$,则sinB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
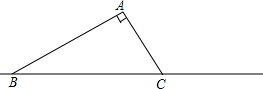 已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求:
已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求: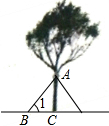 在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).
在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).