题目内容
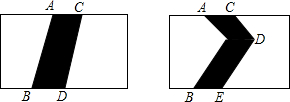如图是两个相同的长方形场地．其中有两条宽度相同的小路，那么这两条小路的面积相等吗？考点：矩形的性质
专题：
分析：过C作CE⊥BE，过D作GH⊥AC，可得：图1中四边形ABCD面积=AC•CE，图2中四边形ABCD面积=AC•DG+AC•DH，根据DG+DH=GH=CE即可解题．
解答：解：过C作CE⊥BE，过D作GH⊥AC，
则图1中，四边形ABCD面积=AC•CE，
图2中，四边形ABCD面积=AC•DG+AC•DH，
∵DG+DH=GH=CE，
∴图1和图2中两条小路面积相等．
则图1中，四边形ABCD面积=AC•CE，
图2中，四边形ABCD面积=AC•DG+AC•DH，
∵DG+DH=GH=CE，
∴图1和图2中两条小路面积相等．
点评：本题考查了平行四边形面积的计算，考查了矩形的性质，本题中求得DG+DH=CE是解题的关键．
练习册系列答案
相关题目
实数4，
，2，|-3|中，最小的是（ ）
| 5 |
| A、4 | ||
B、
| ||
| C、2 | ||
| D、|-3| |
为了考察甲、乙两种树苗的长势，分别各抽取20株树苗，测得其高度并求得它们的方差分别为
=3.6，
=15.8，则（ ）
| S | 2 甲 |
| S | 2 乙 |
| A、甲种树苗的长势比较整体 |
| B、乙种树苗的长势比较整体 |
| C、两种树苗的长势一样整体 |
| D、无法判断 |
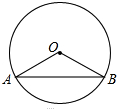如图，⊙O的半径OA=2，AB是⊙O的一条弦，且AB=2
如图，利用一面墙（墙的长度不限），用20米长的篱笆围成一个矩形的花圃，设AB=x，矩形的面积为y．