题目内容
如图：矩形ABCD的长AB=45，宽BC=30．
（1）如图（1），若沿矩形ABCD四周有宽2的环形区域，图中所形成的两个矩形ABCD与A′B′C′D′相似吗？请说明理由．
（2）如图（2），x为多少时，矩形ABCD∽矩形A′B′C′D′？
（1）如图（1），若沿矩形ABCD四周有宽2的环形区域，图中所形成的两个矩形ABCD与A′B′C′D′相似吗？请说明理由．
（2）如图（2），x为多少时，矩形ABCD∽矩形A′B′C′D′？
考点：相似多边形的性质
专题：
分析：（1）先求出A′D′与A′B′的长，再根据相似多边形的对应边成比例即可得出结论；
（2）如果两个矩形ABCD与A′B′C′D′相似，对应边的比相等．就可以求出x的值．
（2）如果两个矩形ABCD与A′B′C′D′相似，对应边的比相等．就可以求出x的值．
解答：解：（1）不相似．
∵矩形ABCD的长AB=45，宽BC=30，
∴A′B′=45-2×2=41，A′D′=30-2×2=26．
∵
=
=
≠
=
，
∴矩形ABCD与A′B′C′D′不相似；
（2）∵矩形ABCD与A′B′C′D′相似，
∴
=
，即
=
，
解得x=3．
∵矩形ABCD的长AB=45，宽BC=30，
∴A′B′=45-2×2=41，A′D′=30-2×2=26．
∵
| AB |
| AD |
| 45 |
| 30 |
| 3 |
| 2 |
| A′B′ |
| A′D′ |
| 41 |
| 26 |
∴矩形ABCD与A′B′C′D′不相似；
（2）∵矩形ABCD与A′B′C′D′相似，
∴
| AB |
| AD |
| A′B′ |
| A′D′ |
| 45 |
| 30 |
| 45-2x |
| 30-2×2 |
解得x=3．
点评：本题主要考查了相似多边形的性质，熟知相似多边形的对应边的比相等是解答此题的关键．
练习册系列答案
相关题目
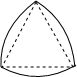如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）| A、π | ||
B、
| ||
| C、2π | ||
D、
|
在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，连接DE，求证：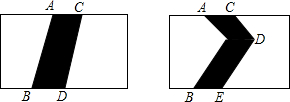
如图是两个相同的长方形场地．其中有两条宽度相同的小路，那么这两条小路的面积相等吗？
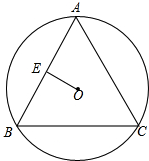如图，⊙O为△ABC的外接圆，AB=AC．若E是AB的中点，连OE，OE=