题目内容
 如图,利用一面墙(墙的长度不限),用20米长的篱笆围成一个矩形的花圃,设AB=x,矩形的面积为y.
如图,利用一面墙(墙的长度不限),用20米长的篱笆围成一个矩形的花圃,设AB=x,矩形的面积为y.(1)求y与x之间的关系式.
(2)求怎样围成一个面积为50m2的矩形花圃?
(3)求出围成矩形最大面积.
考点:二次函数的应用
专题:
分析:(1)由AB=x,就可以得出AD=
,根据矩形的面积公式就可以求出结论;
(2)当y=50时,代入(1)的解析式求出求出x的值即可;
(3)将(1)的解析式化为顶点式就可以求出结论.
| 20-x |
| 2 |
(2)当y=50时,代入(1)的解析式求出求出x的值即可;
(3)将(1)的解析式化为顶点式就可以求出结论.
解答:解:(1)∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
∵AB+BC+AD=20,且AB=x,
∴AD=
,
∴y=x•
=-
x2+10x.
答:y与x之间的关系式为y=-
x2+10x;
(2)当y=50时,
-
x2+10x=50,
解得:x=10.
答:当AB=10时围成的面积为50m2;
(3)∵y=-
x2+10x;
∴y=-
(x-10)2+50.
∴a=-
<0,
∴x=10时,y最大=50.
答:围成矩形最大面积为50平方米.
∴AD=BC,AB=CD.
∵AB+BC+AD=20,且AB=x,
∴AD=
| 20-x |
| 2 |
∴y=x•
| 20-x |
| 2 |
| 1 |
| 2 |
答:y与x之间的关系式为y=-
| 1 |
| 2 |
(2)当y=50时,
-
| 1 |
| 2 |
解得:x=10.
答:当AB=10时围成的面积为50m2;
(3)∵y=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
∴a=-
| 1 |
| 2 |
∴x=10时,y最大=50.
答:围成矩形最大面积为50平方米.
点评:本题考查了矩形的面积公式的运用,二次函数的解析式的运用,由函数值求自变量的值的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
下列问题中,两个变量成反比例函数的是( )
| A、正方形的周长C与它的边长a |
| B、除数一定,被除数和商 |
| C、三角形的面积一定,一边的长a与这边上的高h |
| D、每支铅笔0.5元,买铅笔的支数与总的价钱 |
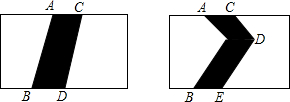 如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?
如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?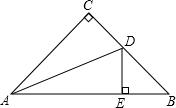 如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.
如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.