题目内容
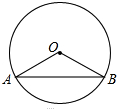 如图,⊙O的半径OA=2,AB是⊙O的一条弦,且AB=2
如图,⊙O的半径OA=2,AB是⊙O的一条弦,且AB=2| 3 |
考点:垂径定理,解直角三角形
专题:
分析:如图,作辅助线,首先证明∠AOC=∠BOC,求出∠AOC=60°即可解决问题.
解答: 解:过点O作OC⊥AB于点C;
解:过点O作OC⊥AB于点C;
则AC=BC=
AB=
×2
=
,
∵OA=OB,
∴∠AOC=∠BOC,
∵sin∠AOC=
=
,
∴∠AOC=60°,∠AOB=120°.
 解:过点O作OC⊥AB于点C;
解:过点O作OC⊥AB于点C;则AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵OA=OB,
∴∠AOC=∠BOC,
∵sin∠AOC=
| AC |
| AO |
| ||
| 2 |
∴∠AOC=60°,∠AOB=120°.
点评:该题主要考查了垂径定理、直角三角形的边角关系及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、解答.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
在一个不透明的塑料袋中装有红色、白色球共20个,除颜色外,其它都相同.小明通过多次摸球实验后发现,其中摸到红球的频率稳定在25%左右.则口袋中红球大约有( )个.
| A、5个 | B、10个 |
| C、12个 | D、15个 |
已知一个样本27,23,25,27,29,31,27,30,32,28,31,28,26,27,29,18,24,26,27,30,那么频数为8的范围是( )
| A、24.5~26.5 |
| B、26.5~28.5 |
| C、28.5~30.5 |
| D、30.5~32.5 |
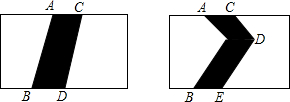 如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?
如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?
 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数.
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数. 如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )
如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )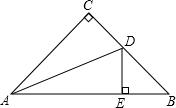 如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.
如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.