题目内容
当m为何值时,关于x的方程
=
-
的解为非正数?
| m |
| (x-2)(x+1) |
| x |
| x+1 |
| x-1 |
| x-2 |
考点:分式方程的解
专题:
分析:根据等式的性质,可把分式方程转化成整式方程,根据解整式方程,可得方程的解,根据方程的解是非正数,可得不等式,根据解不等式,可得答案.
解答:解:方程得两边都乘以(x-2)(x+1),得
m=x(x-2)-(x-1)(x-2).
化简,得
m=x-2.解得x=m+2.
由方程的解为非正数,得
m+2≤0.解得m≤0.
当m=0时,方程的解为2,方程无意义,
当m<0时,关于x的方程
=
-
的解为非正数.
m=x(x-2)-(x-1)(x-2).
化简,得
m=x-2.解得x=m+2.
由方程的解为非正数,得
m+2≤0.解得m≤0.
当m=0时,方程的解为2,方程无意义,
当m<0时,关于x的方程
| m |
| (x-2)(x+1) |
| x |
| x+1 |
| x-1 |
| x-2 |
点评:本题考查了分式方程,先把分式方程转化成整式方程,再求整式方程的解,要检验方程的根.

练习册系列答案
相关题目
 如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )
如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )| A、31 | B、26 | C、25 | D、24 |
下列问题中,两个变量成反比例函数的是( )
| A、正方形的周长C与它的边长a |
| B、除数一定,被除数和商 |
| C、三角形的面积一定,一边的长a与这边上的高h |
| D、每支铅笔0.5元,买铅笔的支数与总的价钱 |
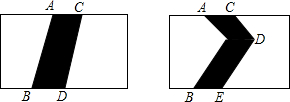 如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?
如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗? 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数.
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数.