题目内容
(1)如图a,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,已知两个正方形的边长相等,当正方形A′B′C′O绕点O转动时,两个正方形重叠部分的面积相等吗?为什么?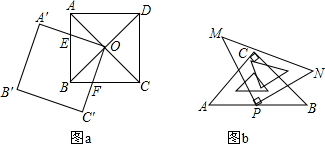
(2)如图(b),△ABC与△PMN是两块全等的等腰直角三角板,当其中一块的直角顶点P绕另一块的斜边中点转动时,两个三角板重叠部分的面积相等吗?为什么?

(2)如图(b),△ABC与△PMN是两块全等的等腰直角三角板,当其中一块的直角顶点P绕另一块的斜边中点转动时,两个三角板重叠部分的面积相等吗?为什么?
考点:全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:(1)易证∠AOE=∠BOF,即可证明△AOE≌△BOF,可得四边形EOFB面积=S△AOB,即可解题;
(2)连接CP,易证∠CPE=∠BPF,即可证明△CPE≌△BPF,可得四边形CEPF面积=S△ACP,即可解题.
(2)连接CP,易证∠CPE=∠BPF,即可证明△CPE≌△BPF,可得四边形CEPF面积=S△ACP,即可解题.
解答:证明:(1)∵AC,BD是正方形ABCD对角线,
∴AO=BO,∠OAE=∠OBF=45°,
∵∠AOE+∠BOE=90°,∠BOE+∠BOF=90°,
∴∠AOE=∠BOF,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(ASA),
∴四边形EOFB面积=S△AOB,
∴两个正方形重叠部分的面积保持不变;
(2)连接CP,

∵△ABC是等腰直角三角形,
∴∠ACP=∠B=45°,CP=BP,
∵∠CPE+∠CPF=90°,∠CPF+∠BPF=90°,
∴∠CPE=∠BPF,
在△CPE和△BPF中,
,
∴△CPE≌△BPF(ASA),
∴四边形CEPF面积=S△ACP,
∴两个三角板重叠部分的面积保持不变.
∴AO=BO,∠OAE=∠OBF=45°,
∵∠AOE+∠BOE=90°,∠BOE+∠BOF=90°,
∴∠AOE=∠BOF,
在△AOE和△BOF中,
|
∴△AOE≌△BOF(ASA),
∴四边形EOFB面积=S△AOB,
∴两个正方形重叠部分的面积保持不变;
(2)连接CP,

∵△ABC是等腰直角三角形,
∴∠ACP=∠B=45°,CP=BP,
∵∠CPE+∠CPF=90°,∠CPF+∠BPF=90°,
∴∠CPE=∠BPF,
在△CPE和△BPF中,
|
∴△CPE≌△BPF(ASA),
∴四边形CEPF面积=S△ACP,
∴两个三角板重叠部分的面积保持不变.
点评:本题考查了全等三角形的判定,考查了全等三角形面积相等的性质,本题中求证△AOE≌△BOF和△CPE≌△BPF是解题的关键.

练习册系列答案
相关题目
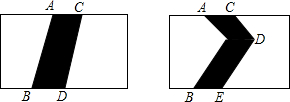 如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?
如图是两个相同的长方形场地.其中有两条宽度相同的小路,那么这两条小路的面积相等吗?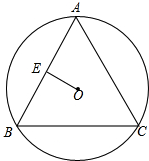 如图,⊙O为△ABC的外接圆,AB=AC.若E是AB的中点,连OE,OE=
如图,⊙O为△ABC的外接圆,AB=AC.若E是AB的中点,连OE,OE= 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数.
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,求∠AOD的度数.