题目内容
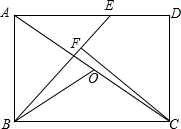 如图,在矩形ABCD中,点E是AD上一点,连接BE,且BE=BC,∠EBC=45°,CF⊥BE于点F,O为AC的中点,AB=2.
如图,在矩形ABCD中,点E是AD上一点,连接BE,且BE=BC,∠EBC=45°,CF⊥BE于点F,O为AC的中点,AB=2.(1)求OB的长;
(2)求证:DE+BF=BC.
考点:矩形的性质,勾股定理,等腰直角三角形
专题:
分析:(1)连接BD,先求得△ABE是等腰直角三角形,根据AB求得BC=BE=
AB=2
,然后根据勾股定理求得BD,进而求得OB的长.
(2)求得△BCE是等腰直角三角形,根据BC求得BF=
BC=2=AB=AE,即可求得结论.
| 2 |
| 2 |
(2)求得△BCE是等腰直角三角形,根据BC求得BF=
| ||
| 2 |
解答: 解:(1)如图,连接BD,
解:(1)如图,连接BD,
∵四边形ABCD是矩形,O是AC的中点,
∴AC、BD交于O,
∴AC=BD,OB=
BD,
∵∠EBC=45°,
∴△ABE是等腰直角三角形,
∴BC=BE=
AB=2
,
∴BD=
=
=2
,
∴OB=
BD=
.
(2)∵CF⊥BE,∠EBC=45°,
∴△BCE是等腰直角三角形,
∴BF=
BC=2
∵△ABE是等腰直角三角形,BE=BC
∴AB=AE=BF=2,
∴BF+DE=AE+DE=AD=BC.
 解:(1)如图,连接BD,
解:(1)如图,连接BD,∵四边形ABCD是矩形,O是AC的中点,
∴AC、BD交于O,
∴AC=BD,OB=
| 1 |
| 2 |
∵∠EBC=45°,
∴△ABE是等腰直角三角形,
∴BC=BE=
| 2 |
| 2 |
∴BD=
| BC2+AB2 |
| 8+4 |
| 3 |
∴OB=
| 1 |
| 2 |
| 3 |
(2)∵CF⊥BE,∠EBC=45°,
∴△BCE是等腰直角三角形,
∴BF=
| ||
| 2 |
∵△ABE是等腰直角三角形,BE=BC
∴AB=AE=BF=2,
∴BF+DE=AE+DE=AD=BC.
点评:本题考查了矩形的性质,等腰直角三角形的判定和性质,勾股定理的应用,等腰直角三角形的判定是本题的重点.

练习册系列答案
相关题目
已知若M=(a+3)(a-4),N=(a+2)(2a-5),其中a为有理数,则M-N的值( )
| A、为正数 | B、为负数 |
| C、为非正数 | D、不能确定 |
 如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2).
如图,在平面直角坐标系内,半径为t的圆D与x轴交于点A(1,0),B(5,0),点D在第一象限,点C的坐标为(0,-2).