题目内容
已知抛物线y=-x2+2x+1的顶点为P,且与x轴交于A、B两点,现将这条抛物线绕原点旋转180°,得到抛物线y=ax2+bx+c且与y轴交于点D,与x轴交于点M、N.
(1)D点的坐标为 .
(2)a= ,b= ,c= .
(3)若点A与N是互相对应的点,试求△PAN的面积.
(1)D点的坐标为
(2)a=
(3)若点A与N是互相对应的点,试求△PAN的面积.
考点:二次函数图象与几何变换
专题:计算题
分析:(1)先把y=-x2+2x+1配成顶点式得y=-(x-1)2+2,则P点坐标为(1,2),再求出点P关于原点的对称点的坐标(-1,-2),由此可得旋转后的抛物线解析式为y=(x+1)2-2,再计算出自变量为0时的函数值即可得到D点坐标;
(2)把y=(x+1)2-2变形为一般式得到y=x2+2x-1,则易得a、b、c的值;
(3)根据抛物线与x轴的交点问题,求出点A与点B的坐标为(
+1,0)、(-
+1,0),点M与点N的坐标为(
-1,0)、(-
-1,0);然后分类讨论:当A(
+1,0),则N(-
-1,0)或当A(-
+1,0),则N(
-1,0),再根据三角形面积公式求解.
(2)把y=(x+1)2-2变形为一般式得到y=x2+2x-1,则易得a、b、c的值;
(3)根据抛物线与x轴的交点问题,求出点A与点B的坐标为(
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:(1)y=-x2+2x+1=-(x-1)2+2,则P点坐标为(1,2),
点P关于原点的对称点的坐标为(-1,-2),
所以旋转后的抛物线解析式为y=(x+1)2-2,
当x=0时,y=1-2=-1,则D点坐标为(0,-1);
(2)y=(x+1)2-2=x2+2x-1,
所以a=1,b=2,c=-1;
故答案为(0,-1);1,2,-1;
(3)当-(x-1)2+2=0,解得x1=
+1,x2=-
+1,则点A与点B的坐标为(
+1,0)、(-
+1,0);
当(x+1)2-2=0,解得x1=
-1,x2=-
-1,则点M与点N的坐标为(
-1,0)、(-
-1,0);
当A(
+1,0),N(-
-1,0),所以△PAN的面积=
×2×(
+1+
+1)=2
+2;
当A(-
+1,0),N(
-1,0),所以△PAN的面积=
×2×(
-1+
-1)=2
-2,
即△PAN的面积为2
+2或2
-2.
点P关于原点的对称点的坐标为(-1,-2),
所以旋转后的抛物线解析式为y=(x+1)2-2,
当x=0时,y=1-2=-1,则D点坐标为(0,-1);
(2)y=(x+1)2-2=x2+2x-1,
所以a=1,b=2,c=-1;
故答案为(0,-1);1,2,-1;
(3)当-(x-1)2+2=0,解得x1=
| 2 |
| 2 |
| 2 |
| 2 |
当(x+1)2-2=0,解得x1=
| 2 |
| 2 |
| 2 |
| 2 |
当A(
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
当A(-
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
即△PAN的面积为2
| 2 |
| 2 |
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
 如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点.若CE的长为2π,BC=8+4
如图,已知四边形ABCD中,AD∥BC,∠C=90°,∠B=30°,以D为圆心,DC为半径的圆交AD于点.若CE的长为2π,BC=8+4 作图题:如图所示是每一个小方格都是边长为1的正方形网格,
作图题:如图所示是每一个小方格都是边长为1的正方形网格, 如图y=-x2+c与x轴相交于A,B两点,顶点C在y轴上,若该抛物线的两个内接正方形ODFE和正方形FHCG如图所示,求c的值.
如图y=-x2+c与x轴相交于A,B两点,顶点C在y轴上,若该抛物线的两个内接正方形ODFE和正方形FHCG如图所示,求c的值.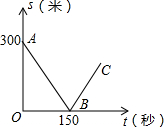 甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题: