题目内容
5.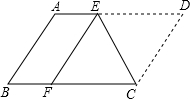 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.
分析 (1)根据折叠的性质得到EF=ED,∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据平行四边形的性质得到EF=AB=4.求得ED=4,得到AE=BF=6-4=2,于是得到结论.
解答 (1)证明:∵将?ABCD沿CE折叠,使点D落在BC边上的F处,
∴EF=ED,∠CFE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴AE∥BF,∠B=∠CFE,
∴AB∥EF,
∴四边形ABFE为平行四边形;
(2)解:∵四边形ABFE为平行四边形,
∴EF=AB=4,
∵EF=ED,
∴ED=4,
∴AE=BF=6-4=2,
∴四边形ABFE的周长=AB+BF+EF+EA=12.
点评 本题考查了平行四边形的判定和性质,折叠的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
16.如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )
| A. | S和C | B. | S和a | C. | C和a | D. | S,C,a |
14. 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
(1)统计表中的x=40,y=0.18;补全条形统计图.
(2)求所有被调查同学的平均劳动时间.
 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)求所有被调查同学的平均劳动时间.
15.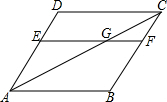 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |