题目内容
14. 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)求所有被调查同学的平均劳动时间.
分析 (1)由频数分布表得到第1组的人数与频率,则可计算出总人数,然后用第3组的频率乘以总人数得到x的值,用总人数除以第4组的频数得到y的值,最后补全条形统计图;
(2)根据加权平均数的公式求解.
解答 解:(1)调查的总人数=12÷0.12=100(人),
所以x=100×0.4=40(人),y=18÷100=0.18,
如图,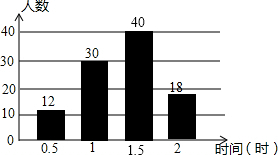
故答案为40,0.18;
(2)所有被调查同学的平均劳动时间=$\frac{1}{100}$(12×0.5+30×1+40×1.5+18×2)=1.32(小时).
点评 本题考查了频数(率)分布表:会条形统计图和频数分布表获取信息.也考查了加权平均数的计算.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
4.有一个多边形,它的内角和等于它的外角和的2倍,则它是( )
| A. | 三边形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
2.若x1、x2是方程x2-2x-1=0的两个根,则x1+x1x2+x2的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
9. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )| A. | 40° | B. | 50° | C. | 60° | D. | 30° |
19.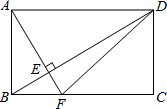 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
6.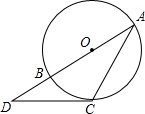 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
3.在Rt△ABC中,∠C=90°,sinA=$\frac{3}{5}$,b=4,则tanB=( )
| A. | $\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
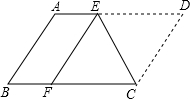 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.