Question

2．探究：如图①，直线l₁∥l₂∥l₃，点C在l₂上，以点C为直角顶点作∠ACB=90°，角的两边分别交l₁与l₃于点A、B，连结AB，过点C作CD⊥l₁于点D，延长DC交l₃于点E．
求证：△ACD∽△CBE．
应用：如图②，在图①的基础上，设AB与l₂的交点为F，若AC=BC，l₁与l₂之间的距离为2，l₂与l₃之间的距离为1，则AF的长度是$\frac{2\sqrt{10}}{3}$．

Answer 1

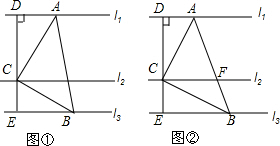
分析 探究：根据已知条件得到∠ADC=∠CEB=90°，于是得到∠ACD+∠DAC=90°，由于∠ACB=90°，于是得到∠ACD+∠ECB=90°，根据余角的性质得到∠DAC=∠ECB，即可得到结论；
应用：通过△ACD≌△BCE，得到AD=CE=1，CD=BE=2，根据勾股定理得到AC=BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，AB=$\sqrt{10}$，然后根据平行线分线段成比例即可得到结论．

解答 探究：证明：∵l₁∥l₃，CD⊥l₁，
∴∠ADC=∠CEB=90°，
∴∠ACD+∠DAC=90°，
∵∠ACB=90°，
∴∠ACD+∠ECB=90°，
∴∠DAC=∠ECB，
∴△ACD∽△CBE；

应用：在△ACD与△CBE中，
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$，
∴△ACD≌△BCE，
∴AD=CE=1，CD=BE=2，
∵∠ADC=CEB=90°，
∴AC=BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∵∠ACB=90°，
∴AB=$\sqrt{10}$，
∵l₁∥l₂∥l₃，
∴$\frac{AF}{AB}=\frac{CD}{DE}=\frac{\sqrt{10}}{3}$，
∴AF=$\frac{2\sqrt{10}}{3}$．
故答案为：$\frac{2\sqrt{10}}{3}$．

点评 本题考查了相似三角形的判定和性质，勾股定理，全等三角形的判定和性质，平行线分线段成比例定理，熟练掌握各定理是解题的关键．