题目内容
7.定义一种运算“*”,其规则为a※b=a2-b2,则方程(x+2)*5=0的解为x1=3,x2=-7.分析 首先根据a※b=a2-b2,可得(x+2)*5=(x+2)2-52,然后解方程(x+2)2-52=0,首先把-52移到方程右边,然后再利用直接开平方法解方程即可.
解答 解:由题意得:(x+2)*5=(x+2)2-52,
(x+2)2-52=0,
(x+2)2=25,
两边直接开平方得:x+2=±5,
x+2=5,x+2=-5,
解得:x1=3,x2=-7.
故答案为:x1=3,x2=-7.
点评 此题主要考查了直接开平方法解一元二次方程,解这类问题要移项,把所含未知数的项移到等号的左边,把常数项移项等号的右边,化成x2=a(a≥0)的形式,利用数的开方直接求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18.绝对值大于3且不大于6的整数有( )
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 8个 |
17.下列各题运算正确的是( )
| A. | 3a+3b=6ab | B. | a+a=a2 | C. | 16a2-9a2=7 | D. | 9ab-9ba=0 |
 已知在纸面上有一数轴(如下图),折叠纸面.
已知在纸面上有一数轴(如下图),折叠纸面. 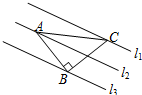 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3,上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是$\sqrt{68}$.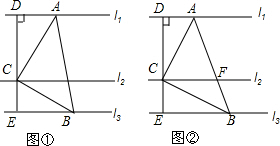
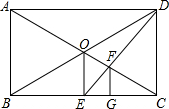 如图所示,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,过点F作FG⊥BC于点G,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O.过点O作OE⊥BC于点E,连接DE交OC于点F,过点F作FG⊥BC于点G,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.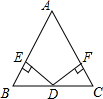 如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.