题目内容
12.已知关于x的方程x2+2x+a=0.(1)若该方程有两个不想等的实数根,求实数a的取值范围;
(2)若该方程的一个根为1,求a的值及该方程的另一个根.
分析 (1)方程有两个实数根,得到根的判别式大于等于0,即可确定出a的范围;
(2)设方程的另一根为x1,根据根与系数的关系列出方程组,求出a的值和方程的另一根.
解答 解:(1)∵方程x2+2x+a=0有两个实数根,
∴△=4-4a>0,
解得:a<1;
(2)设方程的另一根为x1,由根与系数的关系得:
$\left\{\begin{array}{l}{1+{x}_{1}=-2}\\{{x}_{1}=a}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{a=-3}\end{array}\right.$.
则a的值是-3,该方程的另一根为-3.
点评 此题考查了根的判别式,一元二次方程的根,熟练掌握一元二次方程根的判别式与方程根的关系是解本题的关键.

练习册系列答案
相关题目
17.下列各题运算正确的是( )
| A. | 3a+3b=6ab | B. | a+a=a2 | C. | 16a2-9a2=7 | D. | 9ab-9ba=0 |
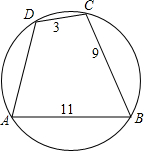 已知圆内接四边形ABCD中,AB=11,BC=9,CD=3,如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$,则AD=7.
已知圆内接四边形ABCD中,AB=11,BC=9,CD=3,如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$,则AD=7. 如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.