题目内容
13.如图1,某人用一张面积为S的三角形纸片ABC剪出一个△EFP,记△EFP得面积为T,已知E,F,P分别是△ABC三边上的三点,且EF∥BC.(1)如图2,若P与B重合,设$\frac{AE}{AB}$分别等于$\frac{1}{2}$,$\frac{1}{3}$,$\frac{3}{4}$时,△PEF的面积分别为T1,T2,T3.
①T1=$\frac{1}{4}$S,T2=$\frac{2}{9}$S,T3=$\frac{3}{16}$S;(用含S的式子表示)
②写出T3的求解过程.
(2)在(1)中T1,T2,T3中的最大值是否是所有满足条件的△EFP(P与B或C不一定重合)的面积的最大值?若不是,求出T的最大值;若是,请给予证明.
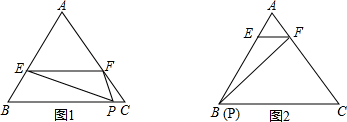
分析 (1)①作AD⊥BC于D,交EF于G,根据相似三角形的判定定理得到△AEF∽△ABC,根据相似三角形的性质得到成比例线段,根据三角形的面积公式计算即可;
②T3的求解过程见①中;
(2)设$\frac{AE}{AB}$=x,根据题意列出二次函数的解析式,根据二次函数的性质求出T的最大值判断即可.
解答  解:(1)①作AD⊥BC于D,交EF于G,
解:(1)①作AD⊥BC于D,交EF于G,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{EF}{BC}$=$\frac{AG}{AD}$=$\frac{AE}{AB}$,
当$\frac{AE}{AB}$=$\frac{1}{2}$时,EF=$\frac{1}{2}$BC,AG=$\frac{1}{2}$AD,则DG=$\frac{1}{2}$AD,
T1=$\frac{1}{2}$×EF×DG=$\frac{1}{4}$S,
当$\frac{AE}{AB}$=$\frac{1}{3}$时,EF=$\frac{1}{3}$BC,AG=$\frac{1}{3}$AD,则DG=$\frac{2}{3}$AD,
T2=$\frac{1}{2}$×EF×DG=$\frac{2}{9}$S,
当$\frac{AE}{AB}$=$\frac{3}{4}$时,EF=$\frac{3}{4}$BC,AG=$\frac{3}{4}$AD,则DG=$\frac{1}{4}$AD,
T3=$\frac{1}{2}$×EF×DG=$\frac{3}{16}$S;
②T3的求解过程见①;
(2)T1,T2,T3中的最大值是所有满足条件的△EFP(P与B或C不一定重合)的面积的最大值,理由如下:
设$\frac{AE}{AB}$=x时,EF=xBC,AG=xAD,则DG=AD-xAD,
T=$\frac{1}{2}$×EF×DG=$\frac{1}{2}$×xBC×(AD-xAD)=(-x2+x)S,
当x=$\frac{1}{2}$时,T有最大值$\frac{1}{4}$S,
所以T1,T2,T3中的最大值是所有满足条件的△EFP(P与B或C不一定重合)的面积的最大值.
点评 本题考查的是相似三角形的判定和性质、二次函数的性质,掌握相似三角形的判定定理和性质定理以及二次函数的性质的应用是解题的关键.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | 在5和6之间 | B. | 在6和7之间 | C. | 在7和8之间 | D. | 在8和9之间 |
| A. | 等边三角形和正六边形 | B. | 正方形和正八边形 | ||
| C. | 正五边形和正十边形 | D. | 正六边形和正十二边形 |
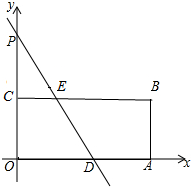 在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12).
在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12).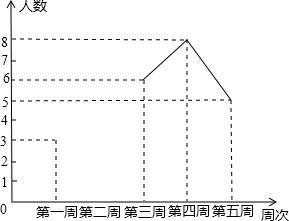 为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
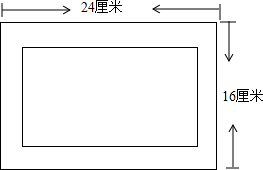 如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米?
如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米? (1)解不等式$\frac{x-1}{3}≤5-x$,并把解集表示在数轴上.
(1)解不等式$\frac{x-1}{3}≤5-x$,并把解集表示在数轴上.