题目内容
4.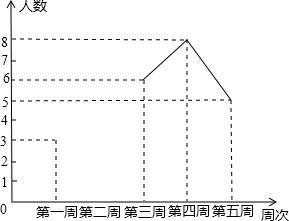 为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:(1)已知这五周“读书之星”人数的众数为8人,求该班这五周“读书之星”人数的平均数;
(2)将折线统计图补充完整;
(3)若第五周的“读书之星”同学中,同学A和B一直坚持得比较好,现在该社会实践活动小组将从第五周的“读书之星”中,随机抽出两位同学谈谈他们的收获,请你用列表或画树状图的方法,求出所选两位同学中至少有一位是同学A或B的概率.
分析 (1)根据众数的定义可得第二周每日都坚持读书的有8人,再根据算术平均数的计算方法进行计算即可得解;
(2)根据第二周每日都坚持读书的有8人补全统计图即可;
(3)设同学分别为A、B、C、D、E,用列表法列出所有可能情况,然后根据概率的定义解答.
解答 解(1)∵众数为8,
∴第二周每日都坚持读书的有8人,
∴其平均人数为$\frac{3+8+6+8+5}{5}$=6;
(2)补全统计图如图所示;
(3)记第五周的5位同学分别为A、B、C、D、E,画树状图如下:
由图可知,共有20种等可能性的情况,其中符合题意的情况有14种.
∴P(至少有一位为A或B)=$\frac{14}{20}$=$\frac{7}{10}$.
点评 本题考查了折线统计图的综合运用,列表法与树状图法,折线统计图表示的是事物的变化情况,根据众数的定义得出第二周每日都坚持读书的有8人是解题的关键.

练习册系列答案
相关题目
14.已知θ为锐角,且$\frac{1}{x}$=1+sinθ,则|2x-1|+|2x-9|的值为( )
| A. | 10 | B. | 8 | C. | 由θ的大小而定 | D. | 无法确定 |
15.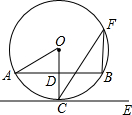 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )| A. | ∠F=$\frac{1}{2}∠AOC$ | B. | AB⊥BF | C. | CE是⊙O的切线 | D. | $\widehat{AC}=\widehat{BC}$ |
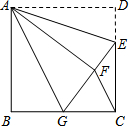 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( ) 如图,已知∠ABC+∠ACB=120°,BO、CO分别是∠ABC与∠ACB的平分线,DE过点O与BC平行,则∠BOC的度数为120°.
如图,已知∠ABC+∠ACB=120°,BO、CO分别是∠ABC与∠ACB的平分线,DE过点O与BC平行,则∠BOC的度数为120°.