题目内容
3.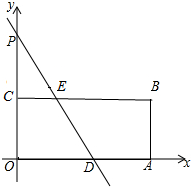 在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12).
在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12).(1)直接写出矩形OABC的周长36;
(2)如图1,过点P的直线与矩形OABC的边OA,BC分别交于点D,E两点,求证:PE=ED.
分析 (1)由四边形OABC是矩形,得到AB=OC,OA=BC,由于OA=12,AB=6,于是得到结果;
(2)由(1)知OC=AB=6,由P(0,12),得到OP=12,求得PC=OP-OC=6,证得PC=OC,根据平行线分线段成比例即可得到结论.
解答 解:(1)∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(12,0),B(12,6),
∴OA=12,AB=6,
∴矩形OABC的周长是2×(12+6)=36;
故答案为:36;
(2)由(1)知OC=AB=6,
∵P(0,12),
∴OP=12,
∴PC=OP-OC=6,
∴PC=OC,
∵CE∥OA,
∴$\frac{PC}{OC}=\frac{PE}{DE}=1$,
∴PE=DE.
点评 本题考查了矩形的性质,矩形周长的求法,平行线分线段成比例定理,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
14.已知θ为锐角,且$\frac{1}{x}$=1+sinθ,则|2x-1|+|2x-9|的值为( )
| A. | 10 | B. | 8 | C. | 由θ的大小而定 | D. | 无法确定 |
15.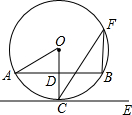 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )| A. | ∠F=$\frac{1}{2}∠AOC$ | B. | AB⊥BF | C. | CE是⊙O的切线 | D. | $\widehat{AC}=\widehat{BC}$ |
 三角形的顶点坐标分别是A(2,2),B(4,2),C(6,4),试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.画出图形并写出各点的坐标.
三角形的顶点坐标分别是A(2,2),B(4,2),C(6,4),试将△ABC缩小,使缩小后的△DEF与△ABC对应边的比为1:2.画出图形并写出各点的坐标.