题目内容
18.如图,直线a∥b,点A为直线a上的动点,点B为直线a,b之间的定点,点C为直线b上的定点.(1)当∠DAB与∠ECB互余(如图1)时,AB与BC存在怎样的位置关系?请说明理由;
(2)在(1)的条件下,将等腰直角三角尺的一个锐角顶点与点B重合放置(如图2).BM平分∠ABP,交直线a于点M.BN平分∠QBC,交直线b于点N.当三角尺绕点B转动,且BC始终在∠PBQ的内部时,∠DMB+∠ENB的值是否变化?若不变,求其值;若变化,求其变化范围;
(3)点F为直线a上一点,使得∠AFB=∠ABF,∠ABC的平分线交直线a于点G,当点A移动时,求$\frac{∠FBG}{∠ECB}$的值.
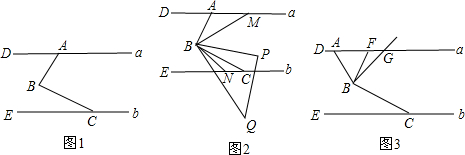
分析 (1)AB⊥BC,过B作BE∥AD,根据平行线的性质得到∠1=∠2,∠3=∠4,于是得到∠1+∠3=∠2+∠4,根据已知条件∠1+∠3=90°,得到∠2+∠4=90°,于是得到结论;
(2)∠DMB+∠ENB的值不变化,由于∠ABQ=∠ABC+∠QBP-∠1=90°+45°-∠1,得到∠ABQ+∠1=135°,根据∠ABQ=∠1+∠ABP+∠QBC,于是得到2∠1+∠ABP+∠QBC=135°,根据角平分线的性质得到∠MBP=$\frac{1}{2}∠ABP,∠NBC=\frac{1}{2}∠QBC$,于是得到2∠1+2∠MBP+2∠NBC=135°即∠1+∠MBP+∠NBC=67.5°,由(1)得∠DMB+∠ENB=∠MBN=∠1+∠MBP+∠NBC,即可得到结果;
(3)根据∠AFB=∠1+∠2,由(1)知∠3=∠2+∠4,由于∠3=∠ABG,于是得到∠2+∠4=∠1+∠ABF,根据∠AFB=∠ABF,推出∠2+∠4=∠1+∠1+∠2,于是得到∠4=2∠1,即可求得结论.
解答  解:(1)AB⊥BC,
解:(1)AB⊥BC,
理由:如图1,过B作BE∥AD,
∵AD∥CE,
∴BE∥CE,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,
∵∠1+∠3=90°,
∴∠2+∠4=90°,
∴∠ABC=90°,
∴AB⊥BC;
(2)∠DMB+∠ENB的值不变化,
理由:如图2,∵∠ABQ=∠ABC+∠QBP-∠1=90°+45°-∠1,
∴∠ABQ+∠1=135°,
∵∠ABQ=∠1+∠ABP+∠QBC,
∴2∠1+∠ABP+∠QBC=135°,
∵∠MBP=$\frac{1}{2}∠ABP,∠NBC=\frac{1}{2}∠QBC$,
∴2∠1+2∠MBP+2∠NBC=135°即∠1+∠MBP+∠NBC=67.5°,
由(1)得∠DMB+∠ENB=∠MBN=∠1+∠MBP+∠NBC,
∴∠DMB+∠ENB=67.5°;
(3)如图3,∵∠AFB=∠1+∠2,
由(1)知∠3=∠2+∠4,
∵∠3=∠ABG,
∵∠ABG=∠1+∠ABF,
∴∠2+∠4=∠1+∠ABF,
∵∠AFB=∠ABF,
∴∠2+∠4=∠1+∠1+∠2,
即∠4=2∠1,
∴$\frac{∠FBG}{∠ECB}$=$\frac{1}{2}$.
点评 本题考查了平行线的性质,三角形外交的性质,角平分线的性质,正确的识别图形是解题的关键.

| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
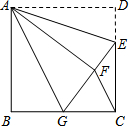 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )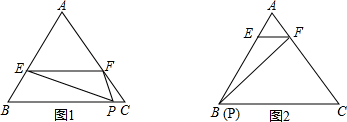
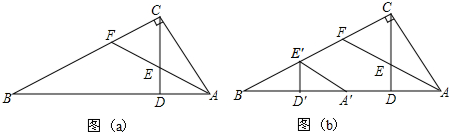
 (1)工程建筑中经常采用三角形的结构,如屋顶的钢架,输电线的支架等,这里运用的三角形的性质是三角形的稳定性;
(1)工程建筑中经常采用三角形的结构,如屋顶的钢架,输电线的支架等,这里运用的三角形的性质是三角形的稳定性; 如图已知△ABC中,∠B和∠C外角平分线相交于点P.
如图已知△ABC中,∠B和∠C外角平分线相交于点P.