题目内容
5.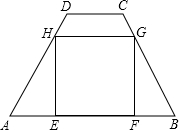 如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.
如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.(1)求四边形ABCD的面积;
(2)设AE=x,矩形EFGH的面积为y,试求y关于x的函数关系式,并求y的最大值;
(3)矩形EFGH能否为正方形?若能,试求该正方形的边长;若不能,请说明理由.
分析 (1)作DM⊥AB于M,CN⊥AB于N,根据勾股定理求出DM,根据梯形的面积公式计算即可;
(2)根据相似三角形的性质用x表示出HE,利用矩形的面积公式计算;
(3)根据正方形的判定定理列出方程,解方程即可.
解答 解:(1) 作DM⊥AB于M,CN⊥AB于N,
作DM⊥AB于M,CN⊥AB于N,
则四边形DMNC为矩形,
∴MN=DC=5,
∴AM=BN=5,
由勾股定理得,DM=$\sqrt{A{D}^{2}-A{M}^{2}}$=12,
则四边形ABCD的面积为:$\frac{1}{2}$×(5+12)×12=102;
(2)∵HE∥DN,
∴$\frac{AE}{AM}$=$\frac{HE}{DN}$,即$\frac{x}{5}$=$\frac{EH}{12}$,
解得,EH=$\frac{12}{5}$x,
∴矩形EFGH的面积y=(15-2x)×$\frac{12}{5}$x=-$\frac{24}{5}$x2+36x,
y=-$\frac{24}{5}$x2+36x=-$\frac{24}{5}$(x-$\frac{15}{4}$)2+$\frac{135}{2}$,
∴y的最大值为$\frac{135}{2}$;
(3)当HE=EF时,矩形EFGH为正方形,
∴$\frac{12}{5}$x=15-2x,
解得,x=$\frac{75}{22}$,
该正方形的边长为15-2×$\frac{75}{22}$=$\frac{90}{11}$.
点评 本题考查的是梯形的性质、二次函数的应用以及相似三角形的判定和性质,掌握二次函数的性质、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
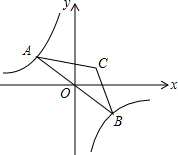 如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.
如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.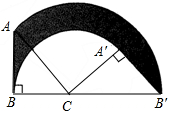 如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.
如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.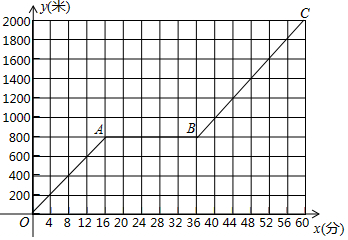 小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.
小明家到公园的路程为2000米,小明爸爸和小明先后从家出发步行去公园.爸爸先出发一直匀速前行,小明在爸爸走出200米后出发,途中他在休闲广场观棋停留一段时间.小明所走路程y(米)与步行时间x(分)的函数图象如图所所示.