题目内容
17.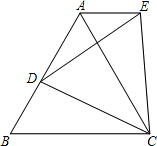 如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证:
如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证:(1)△AEC≌△BDC;
(2)AE∥BC.
分析 (1)首先证明∠BCD=∠ACE,利用SAS即可证得△ACE≌△BCD;
(2)根据SAS证△ACE≌△BCD,推出∠EAC=∠DBC=∠ACB,根据平行线的判定推出即可.
解答 (1)证明:∵△ABC和△EDC是等边三角形,
∴∠BAC=∠DCE=60°,CE=CD,AC=BC,
∴∠BCD=∠ACE,
则在△ACE和△BCD中,
$\left\{\begin{array}{l}{CE=CD}\\{∠BCD=∠ACE}\\{AC=BC}\end{array}\right.$,
∴△AEC≌△BDC(SAS);
(2)∵△ACE≌△BCD(SAS),
∴∠EAC=∠B=60°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
点评 本题考查了等边三角形性质,全等三角形的判定和性质,平行线的判定,关键是求出△ACE≌△BCD,主要考查学生的推理能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
7.如果多项式y2-2my+1是完全平方式,那么m的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 无法确定 |
8.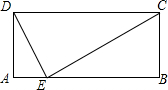 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )| A. | 有一个点 | B. | 有两个点 | C. | 不存在 | D. | 无法确定 |
12.一组数据a、b、c、d、e、f、g的平均数是m,方差是n,则另一组数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数和方差分别是( )
| A. | 2m、2n-3 | B. | 2m-3、n | C. | m-3、2n | D. | 2m-3、4n |
9.下列命题正确的是( )
| A. | 同位角相等 | B. | 如果x2=y2,那么x=y | ||
| C. | 如果a=0,那么ab=0 | D. | 相等的角是对顶角 |
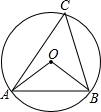 如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.
如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度. 若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )
若正比例函数y=kx的图象如图所示,则一次函数y=x+k的图象大致是( )


