题目内容
5.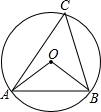 如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.
如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.
分析 由OA=OB,∠OAB=25°,根据等腰三角形的性质,可求得∠OBA的度数,继而求得∠AOB的度数,然后由圆周角定理,求得∠C的度数.
解答 解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°-∠OAB-∠OBA=130°,
∴∠C=$\frac{1}{2}$∠AOB=65°.
故答案为:65.
点评 此题考查了圆周角定理以及等腰三角形的性质.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
13.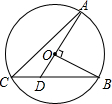 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
20.用四舍五入法取近似数:23.96精确到十分位是( )
| A. | 24 | B. | 24.00 | C. | 23.9 | D. | 24.0 |
10.下列分式变形中,正确的是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | B. | $\frac{-x+y}{x+y}$=-1 | C. | $\frac{(n-m)^{3}}{(m-n)^{2}}$=n-m | D. | $\frac{a}{b}$=$\frac{am}{bm}$ |
14.若一个多边形的内角和是其外角和的4倍,则此多边形的对角线共有( )
| A. | 35条 | B. | 40条 | C. | 10条 | D. | 50条 |
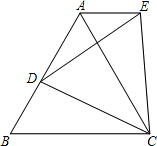 如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证:
如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证: