题目内容
8.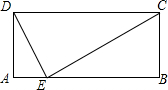 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )| A. | 有一个点 | B. | 有两个点 | C. | 不存在 | D. | 无法确定 |
分析 根据相似三角形的性质得出比例式,设AE=x,得出x的方程,解方程即可得出结果.
解答 解:假设这样的点E存在,设AE=x,
由三个三角形相似知:$\frac{AD}{AE}=\frac{BE}{BC}$,
即$\frac{5}{x}=\frac{12-x}{5}$,
∴x2-12x+25=0,
解得:x=6±$\sqrt{11}$,
即当AE=6+$\sqrt{11}$或AE=6-$\sqrt{11}$时,三个三角形相似,
∴这样的点E有两个.
故选:B.
点评 本题考查了相似三角形的判定与性质、矩形的性质、一元二次方程的解法;由相似三角形的性质得出比例式是解决问题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则应满足的条件是( )
| A. | x≠1 | B. | x=-1 | C. | x=1 | D. | x=±1 |
13.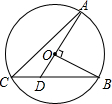 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
20.用四舍五入法取近似数:23.96精确到十分位是( )
| A. | 24 | B. | 24.00 | C. | 23.9 | D. | 24.0 |
 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.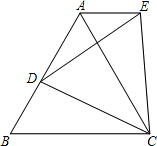 如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证:
如图,△ABC是等边三角形,D是AB上一点,以CD为一边向上作等边△ECD,连接AE.求证: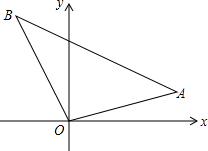 如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题:
如图,Rt△ABO在平面直角坐标系内,A(a,3),B(-4,b).若OA=6,AB=10.回答问题: